How secure would HMAC-SHA3 be?

Question

It would be possible to implement the HMAC construction with (draft) SHA-3, leading to HMAC-SHA3-224, HMAC-SHA3-256, HMAC-SHA3-384, HMAC-SHA3-512 (the last 3 digits are the output size $\ell$, where $\ell/8$ is the $L$ parameter in HMAC). All that's missing to apply the familiar $$\text{HMAC}_K(\text{message})=H(K\oplus\text{opad}\mathbin\|H(K\oplus\text{ipad}\mathbin\|\text{message}))$$ is a definition of the block size $b$, where $b/8$ is the $B$ parameter in HMAC. That is necessary to determine the size of $\text{ipad}$ and $\text{opad}$ (and above what size $K$ needs to be replaced by $H(K)$ beforehand). However, the original and improved security arguments/"proofs" of HMAC are made for the Merkle–Damgård structure, and thus do not directly apply to HMAC-SHA3.

How secure would these HMAC-SHA3-$\ell$ be? What does $b$ needs to be for each of the four $\ell$ values? What kind of security arguments/"proofs" can be made?

Would HMAC-SHA3 be any stronger than the generic sponge MAC?

---

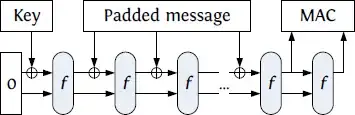
HMAC is briefly discussed in the Keccak submission (section 5.1.3), but I do not understand that a proof is given or a security claim made.

Update: that makes reference to section 5.1.1 which I now read as suggesting that we should have the HMAC blocksize $b$ multiple of the so-called bitrate $r$; thus for output $\ell$ of 224 (resp. 256, 384, 512), $b$ a multiple of 1152 (resp. 1088, 832, 576). That's in agreement with these NIST slides

Answer 1

The Keccak submission says:

From the security claim in [12], a PRF constructed using HMAC shall resist a distinguishing attack that requires much fewer than $2^{c/2}$ queries and significantly less computation than a pre-image attack.

Here, $c$ denotes the capacity of the sponge, i.e. the effective size of the internal state in bits.

Since HMAC is a deterministic iterated MAC (in particular, it does not use a nonce), it is always vulnerable to a generic birthday-based existential forgery attack requiring on the order of $2^{c/2}$ MAC queries (Preneel & Oorschot, 1999).

Thus, the claimed security level of HMAC-SHA3 is the same as the overall maximum attainable security level for HMAC, or any other deterministic iterated MAC construction, with the same effective internal state size.