Basically the same question as Trying to better understand the failure of the Index Calculus for ECDLP but over a different type curve.
There’s a notion of smoothness for hyperelliptic curves, but why is it impossible to solve the Hyperelliptic curve discrete logarithm if the characteristic is large despite a very smooth genus ?
While not an expert in this, it seems that there are improved solutions.
See the paper by Therieault here as well as two sets of slides from a summer school Part 1 and Part 2 by the same researcher.
TL;DR For a curve of genus $g$ the size of the Hyperelliptic Curve group is $q^g,$ where $q$ is the field size. The summary table from the second talk is below:
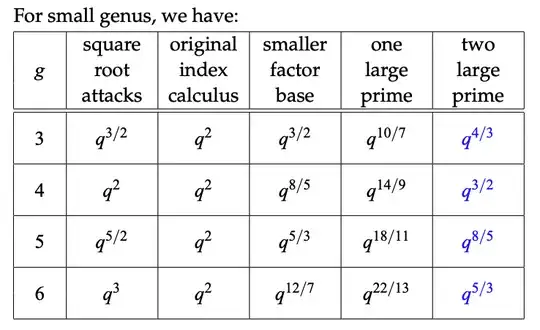
There is improvement when compared to standard Elliptic Curves (the complexities are lower than those of the standard square root algorithms) but not huge improvements. So if we focus on, say genus $g=5,$ so group size $N=O(q^5)$ the original Hyperelliptic Index Calculus has complexity $O(q^2)=O(N^{2/5})$ already, and the improvements to the right go down as much as $O(q^{5/3})=O(N^{1/3}).$
There may have been improvements to the above since then. Granted, these are not subexponential complexities. But there are improvements over elliptic curves if I understood correctly.
