LSFR polynomial next term example

Question

I’m struggling with the mathematical representation of an LFSR as polynomials, and I’d like to understand where I go wrong.

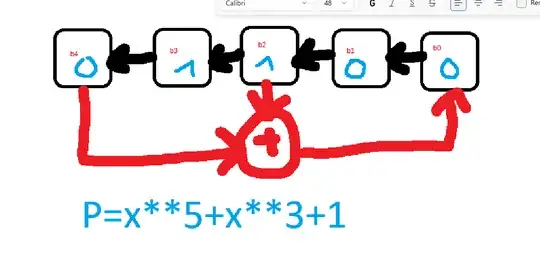
In my example, I use an LFSR with a 5-bit shift to the left and feedback on bits $b_4$ and $b_2$.

My LFSR polynomial is:

$$ P(x) = x^4 + x^2 + 1 $$

Starting with the initial state $(b_4, b_3, b_2, b_1, b_0) = (0, 1, 1, 0, 0)$, we can represent this state as:

$$ S_0(x) = x^3 + x^2 $$

To find $S_1(x)$, I calculated $S_1(x) = (x \cdot S_0(x)) \bmod P(x)$:

$$ S_1(x) = (x^4 + x^3) \bmod P(x) = x^3 + x^2 + 1 $$

This gives me the sequence $(0, 1, 1, 1, 0)$, but I was expecting the sequence $(1, 1, 0, 0, 1)$.

Could someone explain my mistake, please?

I also looked at this answer, which discusses getting the output sequence from the characteristic polynomial. However, I’m confused because, in that example, it seems that $S_1 = x^3$ and then $S_2 = x^3 + 1$, which doesn’t appear to involve a shift.

Edit : I really try my best to understand this answer on this topic but i can't figure out why the states given are valide (How can we have S1=(0,0,0,1) and then S2=(1,0,0,0) i dont see shift here O_O)
Have a great day !

Edit : @fgrieu points that I had the wrong polynomial P(x), it should be $$ P(x) = x^5 + x^2 + 1 $$ I don't know if I should edit directly for the original post ^^

Answer 1

I calculated $S_1(x) = (x\cdot S_0(x))\bmod P(x)$

That's per the formula $S_{i+1}(x) = (x\cdot S_i(x))\bmod P(x)$ to compute the next state of a Galois LFSR, when the drawing is for a Fibonnaci LFSR. Recall that

• in a Galois LFSR the indexes of feedback bits define which state bits are output of XOR gates, and the $x^n$ term of the feedback polynomial represents the bit at the input of each of the $n$ two-inputs XOR gate(s) (with the direct feedback of that bit represented by the $1$ term).
• in a Fibonnaci LFSR, the indexes of feedback bits define the state bits that are are input of XOR gate(s), and a term of the feedback polynomial ($1$ or $x^n$ depending on convention) represents the output of the XOR gate fed into the shift register.

initial state $(b_4,b_3,b_2,b_1,b_0)=(0,1,1,0,0)$ … expecting the (output) sequence $(1,1,0,0,1)$

There are many conflicting conventions about how the output of a LFSR is formed from it's successive states, for both Galois and Fibonnaci LFSRs.

A Fibonnaci LFSR with $n=5$ bits, shifting to the left, with $b_4$ on the left, and feedback bits $b_4$ and $b_2$, has it's state after $(b_4,b_3,b_2,b_1,b_0)$ defined as $(b_3,b_2,b_1,b_0,b_4\oplus b_2)$. The left bit is shifted out, a new right bit equal to the XOR of the feedback bits is added on the right.

Given the stated initial state, it's successive states (including initial) thus are $$(0,1,1,0,0)\\ (1,1,0,0,1)\\ (1,0,0,1,1)\\ (0,0,1,1,1)\\ (0,1,1,1,1)\\ (1,1,1,1,1)\\ (1,1,1,1,0)\\ (1,1,1,0,0)\\ (1,1,0,0,0)\\ (1,0,0,0,1)\\ (0,0,0,1,1)$$

The most common convention for the output is that it's formed by the left bit of the state before shifting, such that the output sequence starts with the initial state. Here that's not the case, but the stated expected output matches the left bit of the state after shifting. Perhaps this is the convention used.

A Galois LFSR with $n=5$ bits, shifting to the left, with $b_4$ on the left, would usually have a feedback bit $b_0$. Otherwise, if it's lowest-numbered bit was $j$, then after $j$ or more steps all bits $0$ to $j-1$ would be zero, and useless. Thus I doubt this is the case.