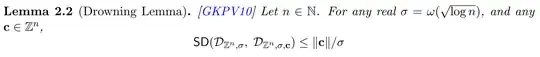Noise flooding in Lattices

Question

I noticed that in the paper [HLL24], the authors used the noise flooding technique to choose parameters and complete the proof.

But I am confused that why set $\sigma \ge 2^{\kappa+6}y$ to guarantee the statistical distance between $\mathcal{D}_{\mathbb{Z},\sigma}$ and $\mathcal{D}_{\mathbb{Z},\sigma,y}$ is less than $2^{\kappa}$?

As I understand, similar to this drowning lemma, the discussing distance is somehow bounded by $\vert y \vert /\sigma$, which leads to $\sigma=\vert y \vert \cdot 2^{\kappa}$. Where did this constant factor $2^6$ come from?

Answer 1

It's not clear to me personally. Let $X\sim \mathcal{D}_{\mathbb{Z},\sigma}$, and let $Y \sim y+\mathcal{D}_{\mathbb{Z},\sigma}$. Let $X(x) \propto \exp(-{\color{red}\pi}\lVert x\rVert_2^2/\sigma^2)$,. This is one of two reasonable normalizations, some authors might instead write $X(x)\propto\exp(-\lVert x\rVert_2^2/(2\sigma^2))$. Regardless of the normalization chosen, we clearly have that $Y(x) = X(x-y)$. For $y\in\mathbb{Z}$, it is simple to see both distributions have the same proportionality constant, so for expressions such as $X(x)/Y(x)$, one may ignore this constant (it cancels).

Anyway, we now bound $\mathsf{SD}(X,Y)$. This is annoying to compute directly (you can try). Instead, one typically appeals to Pinsker's Inequality to write that

$$ \mathsf{SD}(X,Y) \leq \sqrt{\frac{1}{2}\mathsf{KL}(X||Y)}. $$

It is easy to compute

$$ \mathsf{KL}(X||Y) = \mathbb{E}_X[\ln\left(\frac{X(x)}{Y(x)}\right)] = \frac{\pi}{\sigma^2}\mathbb{E}_X[\lVert x- y\rVert_2^2-\lVert x\rVert_2^2] = \frac{\pi}{\sigma^2}\mathbb{E}_X[\lVert y\rVert_2^2 - 2\langle x,y\rangle] = \frac{\pi\lVert y\rVert^2}{\sigma^2}. $$ It then follows that

$$ \mathsf{SD}(X,Y) \leq \sqrt{\frac{\pi}{2}}\frac{\lVert y\rVert}{\sigma}, $$ without a factor $2^6$. If one uses the alternative normalization, you instead get an upper bound of $\frac{\lVert y\rVert}{2\sigma}$, again without a factor of $2^6$.

It is worth mentioning for the second normalization described above, one would require the bound $\sigma \geq \lVert y\rVert_2 2^{\kappa+1}$, so the bound you mention would only be compatible with the first choice of normalization. So there is some nuance here.