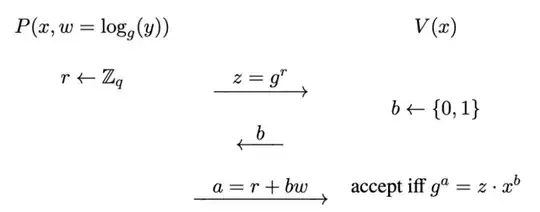Let me try to present a solution. Observe that we need the simulator $S$, given blackbox access to $V^*$ to generate a distribution that is indistinguishable from the view of the adversary $V^*$. This means that $S$ must also produce the challenge bit $b$ according to the distribution used by $V^*$. However, since $S$ only has oracle access to $V^*$, therefore, does not know this distribution. So, our task is to find a method for $S$ to sample from $V^*$ distribution.
Let's simplify this with a basic probability analysis. Let $D$ be a probability distribution over $\{0,1\}$ such that $p_0$ is the probability of sampling $0$ and $p_1 = 1-p_0$ is the probability of sampling $1$. Consider the following sampling algorithm $A$.
- Pick $b \in \{0,1\}$ uniformly at random.
- Sample $b' \gets D$.
- If $(b = b')$, output $b$.
- Else, go to step 1.
Let $P_i$ denote the probability that the algorithm $A$ samples $i$. Let's calculate $P_0$. Note that either $A$ output $0$ in the first iteration if it samples $b = 0$ and $b'$ is also zero, which occurs with probability $\frac{1}{2} \times p_0$. Otherwise, it has failed in the first iteration and repeats. The probability of failure in the first attempt is $\frac{1}{2} p_1 + \frac{1}{2} p_0$ where the two cases are $b=0, b' = 1$ and $b = 1, b' = 0$. Now the interesting part: since, the same process repeats on a failure, the probability of sampling $0$ in any of the subsequent iterations is again $P_0$. Therefore, we get
$$P_0 = \frac{p_0}{2} + \frac{(p_0 + p_1) \times P_0}{2} = \frac{p_0}{2} + \frac{P_0}{2}$$
This implies that $P_0 = p_0$. Similarly, we can show that $P_1 = p_1$.
Observe that $S^{V^*}$ essentially performs the same to simulate the distribution used by $V^*$.
Regarding your question about the type of indistinguishability achieved, it is mentioned in the lecture note that
It is relatively easy to show that $S$ reproduces $V^*$’s view, up to negligible statistical distance.
And this is easily verifiable from the above.
Edit: As @lamontap pointed out, it is possible that the malicious verifier $V^*$ may use different distributions depending on its input $z$. The above calculations do not account for this case.
Let's denote $D_z$ the distribution that $V^*$ will use on input $z$. Let us first calculate the probability that $(z, b, a)$ is the transcript in the real world. Observe that $z$ is chosen uniformly at random by the prover, $b$ is sampled from $D_z$ by the malicious verifier $V^*$, and $a$ is completely determined by $z, b, x$. Therefore, the probability is
$$Pr[z \gets G] \times Pr[b' = b \;|\; b' \gets D_z] = \frac{p_b^z}{q}$$
where $p_b^z$ is the probability of sampling $b$ from $D_z$. In the simulation scenario, the simulator generates this triplet with the following probability which we denote as $p_{z,b,a}^S$. Either
- it generates this in the first iteration with probability $\frac{1}{2} \times \frac{1}{q} \times p_b^z$. This is because even though $z = g^a x^b$, $a$ is chosen uniformly at random. Therefore, $z$ is an element chosen uniformly at random from $G$.
- or it fails in the first iteration but outputs in the subsequent iterations. We can divide the analysis into two cases. Either the simulator sampled $z$ but $b \neq b'$ or it did not sample $z$ and $b \neq b'$. Therefore, the probability is
$$\dfrac{1}{2} \times \dfrac{1}{q} \times (p_0^z + p_1^z)p_{z,b,a}^S + \sum_{y \neq z} \dfrac{1}{2} \times \dfrac{1}{q} \times (p_0^{y} + p_1^y)p_{z,b,a}^S = \dfrac{p_{z,b,a}^S}{2}$$
Combining the above two cases,
$$p_{z,b,a}^S = \frac{p_b^z}{2q} + \frac{p_{z,b,a}^S}{2}$$
and this gives us $p_{z,b,a}^S = p_b^z$.