Message Authentication Code Padding Overview

Question

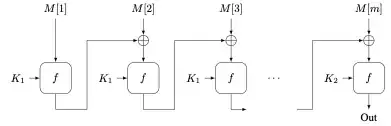
I am confused about padding when using a Message Authentication Code (MAC). This paper suggests using a different key if the message is padded, and otherwise not, which really confused me. An example is the following construction (FCBC MAC):

I want to understand padding in detail, so I will make this question bigger. I try to build it like stepping stones, so please tell me if I forget something!

Fixed-length MAC

The most simple MAC construction everyone learns when doing crypto is CBC MAC; I assume this as common knowledge. CBC MAC is insecure if a probabilistic polynomial time PPT adversary can queue variable length messages to a CBC MAC oracle, breaking nearly all common security definitions.

Variable-length indomain MAC

I use the term indomain if the MAC needs no padding (in other words: if the message length is a multiple of $n$, where $n$ indicates the block size of the MAC). This enables variable message length to some extent. We can achieve this for CBC MAC, when post-computing the CBC MAC output with a differently keyed pseudo-random function PRF (ECBC MAC).

From variable-length indomain to variable-length outdomain MAC

I use the term outdomain for messages that need padding (in other words: the message length is NOT a multiple of $n$, where $n$ indicates the block size of the MAC). Now I get a bit confused.

Edit (so nobody learn something wrong): If I understand John Black and Phillip Rogaway correctly, ECBC MAC is only secure if we don't pad. Otherwise, it is not secure. But why? They don't present an attack in their paper, at least I didn't find it.

The addressed problem in the paper is not "security" but "efficiency"! End Edit

Simplified, their idea is to use a key for the indomain case and a different key for the outdomain case when post-processing the CBC MAC. They call (and prove) this Three-Key Carter-Wegman Construction. Can someone explain to me why this is necessary? Why can't I use the same key for both cases (as long as they are different to the keys used before?).

What happens if we pad somewhere else

In most constructions, padding is done at the end. But what happens when we pad somewhere else, e.g. at the beginning? Or in the middle (which may be complicated to verify)?

Reducing the number of keys

As common practice, I have seen that we can reduce the number of keys by using tag bits (0 bit for all messages before the last, 1 bit for the last message). Doing so, the last PRF does not need to be keyed differently. Can you provide me with a link for a general statement of this concept (e.g. in the Carter Wegman paradigm)? How does this comply with the different keys when padding regarding John Black and Phillip Rogaway's work?

Last but not least, did I forget something about padding?

Answer 1

CBC-MAC is codified by ISO/IEC 9797-1:2011 (free preview at IEC), which has 4 padding methods. If $m$ is the data length in bits and $n$ the block size in bits:

• Padding Method 1: pad with $(-m)\bmod n\;=\;n-1-((m+n-1)\bmod n)$ bit(s) at 0.
• Padding Method 2: pad with a single 1 bit, then $(-(m+1))\bmod n\;=\;n-1-(m\bmod n)$ bits at 0
• Padding Method 3: as in method 1, then a block is prepended coding $m$ in big-endian binary with left-padding to $n$ bits using bit(s) at 0.
• Padding Method 4: either as in Padding Method 1 if $m>0$ and $m\bmod n=0$, or as in Padding Method 2 otherwise. This padding is for use only with MAC Algorithm 5 (which XORs the butlast data block with a spare derived quantity depending on length), also known as CMAC.

Bits are assembled into bytes by big-endian convention, so that for $m$ multiple of 8 the first byte of padding in methods 2 and 3 is 80_h.

This answer does not cover the 6 main variants of CBC-MAC itself, nor truncation of output, nor whatever ISO/IEC 9797-1:2011/Amd 1:2023 might have changed/added.

---

What happens, if we pad somewhere else (than at the end)?

That's what Padding Method 3 does. Prepending a block with the message length guards against the basic message extension attack against the basic CBC-MAC without truncation. But it introduces the huge practical issue that we can't start to compute the MAC until we know the message length. Hence the interest of methods like EMAC or CMAC, which block message extension attack by tweaking the processing at the end of the message.

ECBC MAC is only secure, if we don't pad. Otherwise, it is not secure.

I'm not reading this in John Black and Phillip Rogaway's paper (from the second author's website). My reading is that ECBC MAC is wasteful (doing one more encryption than necessary) but secure if we use Padding Method 2, and would be insecure with just Padding Method 4, but the paper introduces a variant that fixes that.

It does so by using a different key according if Padding Method 4 uses Padding Method 1 or Padding Method 2.

Why can't I use the same key for both cases (as long as they are different to the keys used before?).

This is to avoid that the key used for the final block is the same for two different messages that turn identical after padding. Notice that a message $D$ with length such that $m\bmod n\ne0$, and the larger message $D'$ obtained by padding $D$ per Padding Method 1, both have identical padding per Padding Method 4. A MAC is deterministic (contrary to a Carter-Wegman MAC, which confusingly is not a MAC), so that there is no way that what happened before determines the key used for the final block.

---

If we have a secure variable length "indomain" MAC with block size $n$ and we want to compute the hash of a message $D$ of size $\bigl|D\bigr|$, can we simply append an arbitrary bitstring $X$ to $D$, s.t. $\bigl|D\mathbin\|X\bigr|\bmod n=0$ without losing security?
_{[quoted with some changes for consistency with ISO/IEC 9797-1]}.

No! We need to choose $X$ as a function of $D$ (including possibly, of $\bigl|D\bigr|$) such that the padding transformation $D\mapsto D\mathbin\|X$ is a function (so that in the end the MAC itself is a function, as required). And said transformation must be a surjective function (or computationally collision-resistant, but that's not an option in the context): otherwise $D$ and $D'$ extending $D$ in such way that $D\mathbin\|X\;=\;D'\mathbin\|X'$ would have the same MAC, and that would be exploitable.

Padding Methods 2 and 3 are surjective, Padding Methods 1 and 4 are not. CMAC and the variation of ECBC MAC in the paper use Padding Method 4 for efficiency (saving one block for messages that already are a multiple of the block size), but to compensate the lack of surjectivity of that padding uses two different "indomain" MACs: one uses the surjective Padding Method 2; the other uses Padding Method 1 restricted to cases that nothing is appended, thus the padding transformation is identity, thus surjective.

Answer 2

CMAC is built from a block cipher, so at the lowest level it can only support messages whose length is an exact multiple of the blocklength. Thus, it must use a padding method to encode the input into a padded form that is block-aligned.

If the input is already a multiple of the blocklength, then any padding method will add an entire extra block of padding. The extra block leads to an extra call to the PRF, and it is natural to wonder whether this cost can be avoided. It is indeed inevitable when using padding for encryption, because the receiver must be able to unambiguously recover the original message. But in a PRF/MAC, both "signer" and verifier already hold the entire message. Their only goal is to "do something different" for all messages, which could be possible using an approach other than padding.

CMAC's approach is to use a different key when the input is already a multiple of the blocklength. It's a little bit like the following:

$$ F'\bigl(K_1 \| K_2, M\bigr) = \begin{cases} F(K_1,\textsf{Pad}(M)) & \text{ if } M \text{ not a multiple of the blocklength} \\ F(K_2, M) & \text{ if } M \text{ is a multiple of the blocklength}\end{cases}$$

So in the case where $M$ is already a multiple of the blocklength, we don't pad, meaning we don't add an extra block. Instead, we just use a different key. It's hopefully relatively clear why this construction is a secure MAC/PRF -- these two cases (what you call "indomain" and "outdomain") are handled by completely different keys.

The only problem with this simplified $F'$ is that you have to know the length of $M$ before you start, to know which key to use. CMAC gets around this because the underlying $F$ already uses 2 keys (it is a Carter-Wegman-like design), and only "finalization" key needs to change based on the two cases. So you can start the computation before knowing the length of $M$, and only at the end decide which finalization key to use based on its length.