I have modified a quantum-quantum multiplication operator to do what you're looking for.
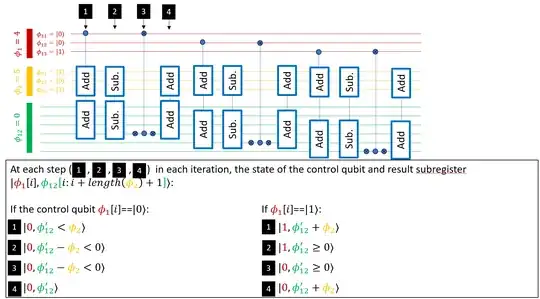
for i in range(length(\phi_1)):
output_subregister = \phi_{12}[i:i+length(\phi_1)+1]
if \phi_1[i] == 1:
output_subregister += \phi2
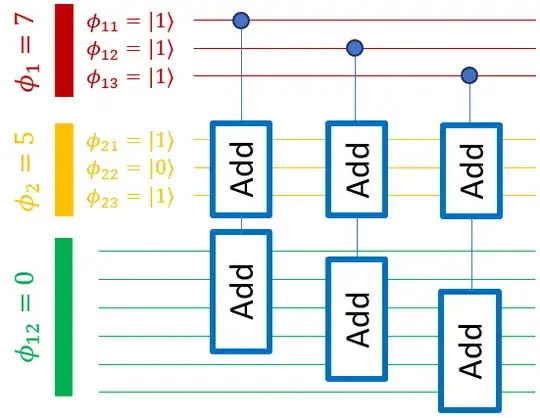
We can start from this quantum-quantum multiplier, which pseudocode is given above. Adding $\phi_2$ to a subset of qubits in $\phi_{12}$ like such, will successively add $2^{i-1}\phi_2$ to the register $\phi_{12}$, controlled by the $i^{th}$ qubit in register $\phi_1$. For those unfamiliar, this is because the product $\phi_1 \phi_2$ can be decomposed into the sum $\phi_2(2^0\phi_{11} + 2^1\phi_{12} + ... 2^{n-1}\phi_{1n}$), where $\phi_{1i} \in \{0,1\}$ is the state of the $i^{th}$ qubit in $\phi_1$. This produces the state $|a,b,0\rangle \rightarrow |a,b,ab\rangle$.
Example implementations of the addition operation are described in these two papers: https://arxiv.org/pdf/quant-ph/0008033 or https://arxiv.org/pdf/quant-ph/9511018. Note the +1 qubit in the output_subregister - that is to account for the fact that an addition of two $n$-bit numbers might potentially produce a $(n+1)$-bit result.
To uncompute the control qubit $\phi_{1i}$ at the $i^{th}$ step of the iteration, we can utilize two observations:
- At the start of the iteration step (before adding $\phi_2$), output_subregister will always store a value less than $\phi_2$. This can be verified by noticing that the current cumulative sum in the entire $\phi_{12}$ register will be $\phi_2(2^0 + 2^1 + ... 2^{i-1})$. The value in the subregister will be a right bit-shift of this value by $i$ bits, which will be $\leq\phi_2(2^{-i} + 2^{-i+1} + ... 2^{-1})$.
- When subtracting a $b$ from $a$ using an inversion of either of the two examples of the quantum adders described above (using negative angles in https://arxiv.org/pdf/quant-ph/0008033, reversing the order of all gates in https://arxiv.org/pdf/quant-ph/9511018), an underflow will occur when $b>a$. This is indicated by the most significant $(n+1)$ qubit in the output register being in the $|1\rangle$ state.
Considering these two, we can subtract $\phi_2$ from the subregister of $\phi_{12}$ to "test" whether the control qubit $\phi_{1i}$ was in the $|1\rangle$ state. If $\phi_{1i}$ was in the $|1\rangle$ state, $\phi_2$ would have been previously added to the output subregister, and subtracting $\phi_2$ at this step would leave the value positive. Whereas if $\phi_{1i}$ was in the $|0\rangle$ state, subtracting $\phi_2$ would cause an underflow and result in the most significant $(n+1)$ qubit in the result subregister to be $|1\rangle$. We can use this qubit to control a CNOT applied on the control qubit, to set it to $|0\rangle$ if it was previously $|1\rangle$. This effectively erases the value stored in $\phi_1$ as we proceed along in calculating the product $\phi_1 \phi_2$. This produces the state $|a,b,0\rangle \rightarrow |0,b,ab\rangle$. We can very well swap the first and third register to get the state you want.
for i in range(length(\phi_1)):
output_subregister = \phi_{12}[i:i+length(\phi_1)+1]
if \phi_1[i] == 1:
output_subregister += \phi2
output_subregister -= \phi2
if output_subregister[-1] == 0: #indicates an underflow from the previous subtraction
#Occurs only if \phi2 was added, which means \phi_1[i] == 1
\phi_1[i] = NOT \phi_1[i]
output_subregister += \phi2
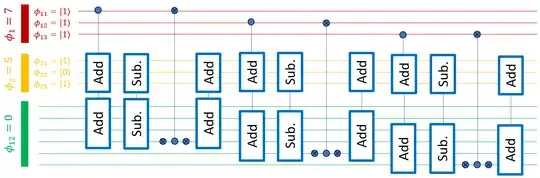
We can trace the states throughout one step of the iteration and verify it is indeed what we want for both possible values of the control qubit in superposition.