4

The Elitzur-Vaidman [EV] bomb tester, first described in 1993, is a wonderful "pre-Shor's algorithm" application of quantum information. The original paper is written in the language of Mach-Zhender interferometers, beam splitters, detectors, and an amount of transparency of a silvered mirror, and doesn't use the terms qubit or quantum gates but instead for example refers to a photon going to the "right" as $|1\rangle$, and going "up" as $|2\rangle$. The paper contends that optimally they can test about one half of all live bombs without causing an explosion.

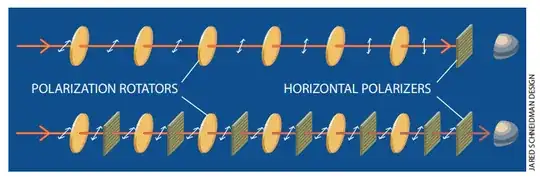
However, Kwiat, Weinfurter, and Zeilinger [KWZ] describe an improved bomb tester in a Scientific American article from 1996, titled "Quantum Seeing in the Dark". This can test for the presence of a live bomb with arbitrary accuracy, by reusing the photon and relying on the quantum Zeno effect to freeze the photon in a particular basis. Although Elitzur and Vaidman also considered reusing a photon, the improvement of [KWZ] posits to rotate the photon by an amount $\epsilon$ if the bomb is a dud (and to have it reset if the bomb is live).

Quantum Seeing in the Dark

I really love this improvement, as it naively seems counter to many hypotheses about where and why quantum computers can algorithmically outperform classical computers. In the tester as described in [KWZ], there is only a single qubit, which shouldn't be entangled to anything$^\dagger$, and yet there seems to be something nontrivially achieved over and above what can be done classically.

From whence does the power of [KWZ], which only uses a single qubit and relies on the quantum Zeno effect, come?

Are there a lot of air-quotes in my assessment above? For example is there really an "improvement" over what's achievable classically, or is it nonsense to consider a classical bomb tester? Is this improvement merely a parlor trick and not an "algorithm", or is it as I suspect more profound than that? If we were to pray at the Church of the Higher Hilbert Space would we find that the qubit that gets rotated is in actuality "entangled" with whether or not the bomb is live or a dud?

Although a careful reading of [KWZ] notes that they do use downcoversion to create entangled photons, this only appears to aid in their experimental setup and is not critical for the algorithm.

Mark Spinelli
  • 15,789
  • 3
  • 26
  • 85

1 Answers1

1

I just want to contribute with some information that might help by exploring the question "what is an improvement of quantum over classical?".

It is possible to reproduce the phenomenology of the E-V Bomb Tester in the Spekkens Toy Theory, which is an epistemically restricted classical theory. In terms of the language used in Bell's theorem, the Spekkens toy theory is a local hidden variable theory. By construction, this theory is easy to simulate in a classical computer. You can see the argument in the paper "Why interference phenomena do not capture the essence of quantum theory". Therefore, the simple phenomenology of "it is possible to detect that a bomb is good without exploding it" does not show any quantum advantage.

Even though the phenomenology of the E-V Bomb Tester that is traditionally considered "weird" can be explained by this toy theory, in a follow up paper called "Aspects of the phenomenology of interference that are genuinely nonclassical" the authors show that there are more detailed/quantitative aspects of the phenomenology of these simple interferometers that do show quantum advantage, in the sense that they provide proofs of generalized contextuality. The paper "Coherence and contextuality in a Mach-Zehnder interferometer", by different authors, also shows aspects of interferometer phenomenology that show contextuality. I haven't read these last two papers so I'm not sure whether they treat the KWZ generalization of the E-V bomb tester.

Relating back to your question, these last two papers can show contextuality from interferometer phenomena because, to show contextuality, it is not necessary to have entangled states. For example, in the original paper that defined generalized noncontextuality, "Contextuality for preparations, transformations, and unsharp measurements", there are various proofs of contextuality for 2d Hilbert spaces (that is, using only one qubit).

There is a lot of people that work in the connections between contextuality and quantum advantage in computation, but I don't know enough about it to provide good references. Because of that I cannot answer your question fully, but I hope the references I provided are useful!

Marina
  • 11
  • 1