What is the relation between braiding and CNOT?

Question

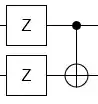
According to Fowler, Mariantoni, Martinis, and Cleland, 2012, Surface codes: Towards practical large-scale quantum computation (PRL link, page 29), braiding transformations are doing the same thing that CNOT and its adjacent are doing to 2Q gates:

$$\hat{CNOT}\:^\dagger\big(\hat I\otimes\hat X\big)\hat{CNOT}\:^=\hat I\otimes \hat X,\\ \hat{CNOT}\:^\dagger\big(\hat X\otimes\hat I\big)\hat{CNOT}\:^=\hat X\otimes \hat X,\\ \hat{CNOT}\:^\dagger\big(\hat I\otimes\hat Z\big)\hat{CNOT}\:^=\hat Z\otimes \hat Z,\text{and}\\ \hat{CNOT}\:^\dagger\big(\hat Z\otimes\hat I\big)\hat{CNOT}\:^=\hat Z\otimes \hat I.$$

which is exactly what a braiding transformation is doing.

And they say that therefore, braiding is analogous to CNOT.

But I say no! - it is analogous to $$\hat{CNOT}\:^\dagger\big(2Qubit Operator)\hat{CNOT}\:^.$$ which is 2 CNOTs, and not one CNOT!

Can someone settle this for me please?

Thank you!

Answer 1

They are considering the adjoint action of CNOT, i.e. its action as a quantum channel on density matrices, see also this recent question.

Since the Pauli operators form a basis for the vector space of linear operators, it is enough to know the action of a quantum channel on those. Moreover, for unitaries, it is even enough to know it on a set of generators of the Pauli group, like in this case $I\otimes X, X\otimes I, I\otimes Z, Z\otimes I$. This is because we have $$ U PQU^\dagger = UPU^\dagger UQU^\dagger, $$ so the image of $PQ$ is simply the product of the images of $P$ and $Q$.

This is a very common thing to do, especially if you are dealing with Clifford gates.

Hence, braiding effectively gives you the same quantum channel as a CNOT gate. This determines the underlying unitary up to a global phase. But since the latter is anyway not measurable, this is completely fine.

Answer 2

[Paraphrased: Why does $C^\dagger P C$ use $C$ twice? In the circuit it's only there once!]

Consider a Pauli product $P = Z \otimes Z$ before a CNOT $C$ in a quantum circuit:

We want to know what the CNOT transforms this Pauli product into. We want to know what the Pauli product becomes on the right hand side of the CNOT:

Note that it is always the case that $C^\dagger C = I$. In other words, we can insert a pair of CNOTs anywhere into the circuit and not change it:

But, in the middle expression, notice we can now switch our focus from "the original CNOT is the rightmost CNOT" to "the original CNOT is the leftmost CNOT". Meaning the series of operations $CNOT \cdot (Z \otimes Z) \cdot CNOT$ must equal our mystery product. And the reason there's a pair of them is because we inserted a pair of self-cancelling operations to allow ourselves to shift focus.

---

Another way to understand what is happening is to realize that saying

$$P_{after} = C P_{before} C^\dagger$$

is the same as saying (right multiply by $C$):

$$P_{after} \cdot C = C P_{before} C^\dagger C$$

which is the same as saying (cancel $C^\dagger C = I$)

$$P_{after} \cdot C = C \cdot P_{before}$$

In words: there was a matching mystery for why $P_{after}$ had NO cnots, instead of 1 cnot. It turns out the missing cnot was the extra cnot beside $P_{before}$. The equation was originally telling us how to move the one CNOT from one side of the Pauli product to the other, and then we solved for $P_{after}$ which rearranged things.

Answer 3

A quote in Fowler, Mariantoni, Martinis, and Cleland, 2012, "Surface codes: Towards practical large-scale quantum computation" (page 22) a few pages earlier than my question. I refer to the CNOT as the unitary operation, and to the middle 2Q operation as the not unitary A. So: