Writing Toffoli Gate Matrix by one and two qubit gate matrices

Question

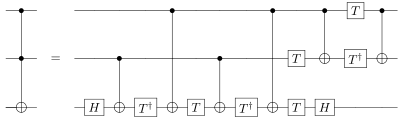
I am trying to write Toffoli gate matrice by using one and two qubit gates matrices. I follow this circuit

link for the circuit

I first started to write the matrices of one and two qubit gates:

identity = np.array([[1, 0], [0, 1]])
xgate = np.array([[0, 1], [1, 0]])
ygate = np.array([[0,-1j],[1j,0]])
zgate = np.array([[1,0],[0,-1+0j]])
hgate = 1/math.sqrt(2)*(xgate+zgate)
sgate = np.sqrt(zgate)
tgate = np.sqrt(sgate)
tdag = tgate.conj().T
cnot = 0.5*(np.kron(identity,identity)+np.kron(identity,xgate)+np.kron(zgate,identity)-np.kron(zgate,xgate))
deneme = np.kron(identity, swap)
deneme2 = np.kron(cnot,identity)
deneme3 = np.kron(identity,swap)
#deneme_ = deneme*deneme2*deneme3
deneme_ = np.matmul(deneme,deneme2)
non_adjacent  = np.matmul(deneme_,deneme3)

Then, I started to write each part of the circuit in the following way:

tof1 = np.kron(np.kron(identity,identity),hgate)
tof2 = np.kron(identity,cnot)
tof3 = np.kron(np.kron(identity,identity),tdag)
tof4 = non_adjacent
tof5 = np.kron(np.kron(identity,identity),tgate)
tof6 = np.kron(identity,cnot)
tof7 = np.kron(np.kron(identity,identity),tdag)
tof8 = non_adjacent
tof9 = np.kron(np.kron(identity,tdag),tgate)
tof10 = np.kron(cnot,hgate)
tof11 = np.kron(np.kron(identity,tdag),identity)
tof12 = np.kron(cnot,identity)
toffoli = tof1*tof2*tof3*tof4*tof5*tof6*tof7*tof8*tof9*tof10*tof11*tof12

And the final matrix is that:

My guess is that: I did a mistake when I tried to write cnot gate for the first and third qubits or maybe I am wrong to write identities

Can someone explain to me what I missed? Sorry for this dumb question Thanks in advance

Answer 1

Here I am providing working code:

import numpy as np
import math as m
idn = np.array([[1, 0], [0, 1]])
h = (1/m.sqrt(2))*np.array([[1, 1], [1, -1]])
t =    np.array([[1, 0], [0, (1/m.sqrt(2))*(1+1j)]])
tdag = np.array([[1, 0], [0, (1/m.sqrt(2))*(1-1j)]])
cnot_adj = np.array([[1, 0, 0, 0],
                     [0, 1, 0, 0],
                     [0, 0, 0, 1],
                     [0, 0, 1, 0]])
cnot_non_adj = np.array(
                        [[1, 0, 0, 0, 0, 0, 0, 0],
                         [0, 1, 0, 0, 0, 0, 0, 0],
                         [0, 0, 1, 0, 0, 0, 0, 0],
                         [0, 0, 0, 1, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 1, 0, 0],
                         [0, 0, 0, 0, 1, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 1],
                         [0, 0, 0, 0, 0, 0, 1, 0],
                        ]
                        )
toffoli = np.kron(np.kron(idn, idn), h)
toffoli = np.dot(np.kron(idn, cnot_adj), toffoli)
toffoli = np.dot(np.kron(np.kron(idn, idn), tdag), toffoli)
toffoli = np.dot(cnot_non_adj, toffoli)
toffoli = np.dot(np.kron(np.kron(idn, idn), t), toffoli)
toffoli = np.dot(np.kron(idn, cnot_adj), toffoli)
toffoli = np.dot(np.kron(np.kron(idn, idn), tdag), toffoli)
toffoli = np.dot(cnot_non_adj, toffoli)
toffoli = np.dot(np.kron(np.kron(idn, t), t), toffoli)
toffoli = np.dot(np.kron(cnot_adj, h), toffoli)
toffoli = np.dot(np.kron(np.kron(t, tdag), idn), toffoli)
toffoli = np.dot(np.kron(cnot_adj, idn), toffoli)
np.set_printoptions(precision=3) #"rounding"
np.set_printoptions(suppress=True) #supressing scientific format"
print('Real parts')
print(toffoli.real)
print('\nImaginary parts')
print(toffoli.imag)

Variable cnot_non_adj is CNOT gate with control on the uppermost qubit and target on the lowermost qubit. The matrix is designed according to manual I provided here.

Note that np.dot is a matrix multiplication. You can see, that the order in the multiplication is reversed in comparison with the diagram.

The result of the code is

Real parts
[[1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0.]
 [0. 0. 0. 0. 1. 0. 0. 0.]
 [0. 0. 0. 0. 0. 1. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 0. 0. 0. 1. 0.]]
Imaginary parts
[[-0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0. -0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0. -0. -0.]
 [ 0.  0.  0.  0.  0.  0. -0. -0.]]

This is a matrix description of the Toffoli gate.