3
  • Give an example of a continuous function $f:R\rightarrow R$ which attains each of its values exactly three times.

Ed.: answered by the duplicate above

  • Does there exist a continuous function $f:R\rightarrow R$ which attains each of its values exactly two times?

Ed.: answered by $f: \mathbb{R} \to \mathbb{R}$ that takes each value in $\mathbb{R}$ twice

Community
  • 1
user154990
  • 155
  • http://math.stackexchange.com/questions/730692/f-mathbbr-to-mathbbr-that-takes-each-value-in-mathbbr-twice/730712#730712 – Seth Aug 12 '14 at 17:52
  • 2
    I think this is a duplicate. – Git Gud Aug 12 '14 at 17:52
  • http://math.stackexchange.com/questions/735842/function-f-mathbbr-to-mathbbr-that-takes-each-value-in-mathbbr-th?rq=1 – Seth Aug 12 '14 at 17:53
  • think about a $\sin x$ function on an appropriate interval – Avitus Aug 12 '14 at 17:59
  • thank you all for helping me. – user154990 Aug 12 '14 at 17:59
  • 1
    It is not an exact duplicate, because the other question do not ask to exhibit a function with the property that any value in the image is took three times. – Jack D'Aurizio Aug 12 '14 at 18:21
  • 1
    Neither it is a duplicate of the other question, it is just both of them. It would have some sense to merge the three questions into this topic. – Jack D'Aurizio Aug 12 '14 at 22:41
  • I don't know about merging; another reason it is not a duplicate of the other "three times" question is because that one did not ask for continuity. Although this question did get answered there, I don't know that that is enough to make the more difficult question a duplicate of the other. – Jonas Meyer Aug 13 '14 at 02:13

1 Answers1

5

$$f(x)=2\left\lfloor\frac{x}{3\pi}\right\rfloor-\cos\left(3\pi\left\{\frac{x}{3\pi}\right\}\right)\tag{1}$$ is a differentiable function that attains any real value in exaclty three points, whose graphics is the following one:

$\hskip2in$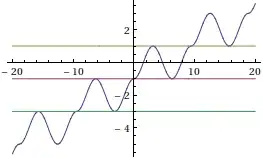enter image description here

If in $(1)$ you replace "$3$" with the positive odd integer $2m+1$, you get a $C^1$-function that attains any real value in exactly $2m+1$ points. You can also take:

$$f(x) = T_{2m+1}\left(x-2\left\lceil\frac{x-1}{2}\right\rceil\right)+2\left\lceil\frac{x-1}{2}\right\rceil,$$

where $T_{2m+1}$ is the $(2m+1)$-th Chebyshev polynomial of the first kind. This is a $C^1(\mathbb{R})$ function, too.

You cannot have a continuous function $g$ that takes any value in $g(\mathbb{R})$ exactly twice. Such function cannot be monotonic, hence must have a point $x_0$ of local maximum/minimum and another point $x_1\neq x_0$ for which $g(x_1)=g(x_0)$. Then, by continuity, there exists a constant $G$ sufficiently close to $g(x_0)$ but different from $g(x_0)$ such that there are two points $y_1,y_2$ in a neighbourhood of $x_0$ (because $x_0$ is a maximum/minimum), and at least one point $y_3$ in a neighbourhood of $x_1$ such that $$ g(y_1)=g(y_2)=g(y_3)=G,$$ contradiction.

Jack D'Aurizio
  • 361,689