There is a problem that killed me! but I couldn't solve it: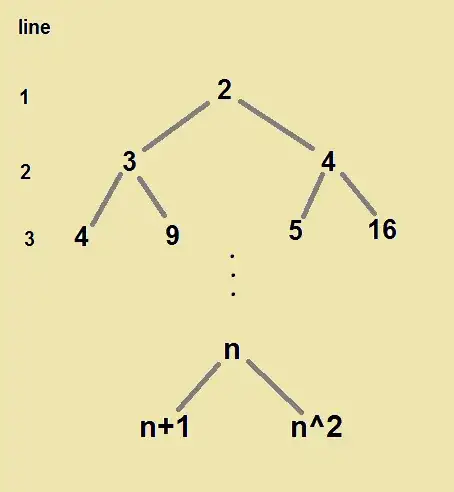
We have a tree graph witch its structure is what is on image. Proof that there is no reduplicative numbers in each line.
There is a problem that killed me! but I couldn't solve it:
We have a tree graph witch its structure is what is on image. Proof that there is no reduplicative numbers in each line.
First, let's start with a self-evident lemma: every number on line $i$ is greater than $i$.
Suppose by way of contradiction that line $i$ is the first line where an integer $n$ appears twice. One $n$ must come from squaring and the other one must come from adding $1$, because if they were both produced from the same method, then $i - 1$ would be an earlier line where this phenomenon happens.
Let's say that $n$ is the $j$th square, where $1$ is first in the sequence of squares. (In other words, $ j = \sqrt{n}$.) Then the $j-1$th square is $n - (2j - 1)$.
Consider the $n$ that comes from adding $1$. The fastest (requiring the least number of lines) way to make that $n$ is to start with the $j-1$th square and add $1$ every line until you reach $n$. Thus the $j-1$th square appeared at least $(2j - 1)$ lines before line $i$.
Now consider the $n$ that comes from squaring. Then on line $i-1$, we have $\sqrt{n} = j$. So $j$ occurs on the $i-1$th line, but we know that $i - 1 \geq (2j - 2)$ because we've identified a number that must be occur $(2j - 1)$ lines before line $i$. Since $ j < (2j - 2)$, this contradicts our lemma.