17

Is it possible to divide an equilateral triangle into 5 equal (i.e., obtainable from each other by a rigid motion) parts?

Ivan Neretin
  • 13,429
Jaska
  • 1,299

2 Answers2

24

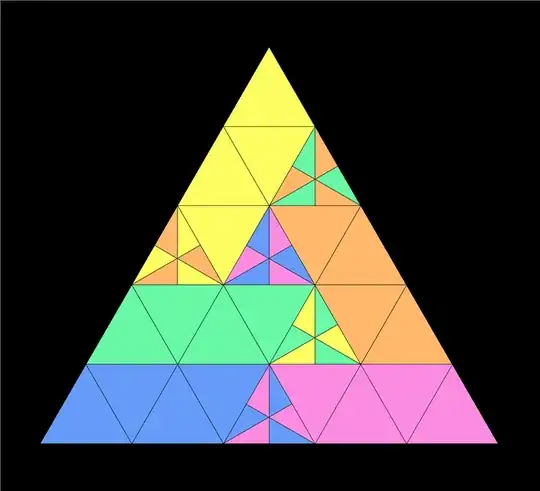
The answer is "yes", it is possible to divide equilateral triangle into $5$ equal parts, see the picture below which comes from here: https://ru-math.livejournal.com/831851.html

enter image description here

naXa stands with Ukraine
  • 103
  • 4
Sergey Markelov
  • 496
  • 1
    Note: one of the figures has to be reflected to match others. The OP says "I think it [reflection] does not leave the arrangement of triangle angles unchanged so no [reflection is not counted as rigid motion]." – naXa stands with Ukraine Jan 06 '19 at 18:52
8

You might want to look at:

http://www.michaelbeeson.com/research/papers/TriangleTiling1.pdf

and the references given there.

Grigory M
  • 18,082
Joseph Malkevitch
  • 5,115
  • In particular, look at the pinwheel tiling, which is for right triangles. See http://en.wikipedia.org/wiki/Pinwheel_tiling – lhf Oct 30 '10 at 02:18
  • 2
    Umm. I was looking a solution for equilateral triangle so how right triangle helps me? – Jaska Oct 30 '10 at 12:02
  • It seems that, according to Theorem 7 (on page 116) of the reference given by Joseph Malkevitch, the answer to your question is "no." – JRN Nov 16 '11 at 03:59
  • 1
    http://www.michaelbeeson.com/research/papers/TriangleTiling1.pdf#page=56 (updated url) – Lam Chau Oct 24 '12 at 03:33