Why is $\cos (90)=-0.4$ in WebGL?

Question

I'm a graphical artist who is completely out of my depth on this site.

However, I'm dabbling in WebGL (3D software for internet browsers) and trying to animate a bouncing ball.

Apparently we can use trigonometry to create nice smooth curves.

Unfortunately, I just cannot see why.

I can accept this diagram:

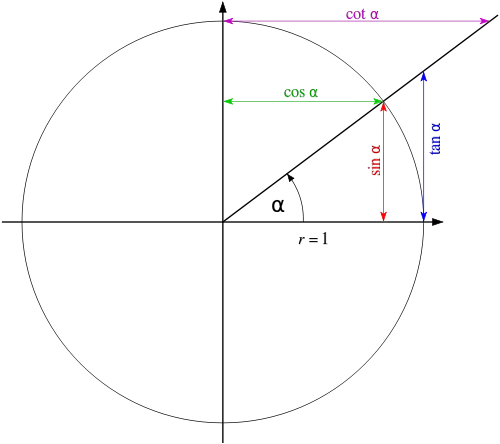
triangles and circle

However, running some calculations just do not make sense to me:

Let's set $\alpha$ to 45 (around where it appears to be in the diagram) and find the cosine value, thus giving us the green line. $$\cos(45) = 0.5$$

Fair enough. $\cos(\alpha)$ / the green line is $0.5$ units.

But now this is where it all falls apart. I would have thought if we set $\alpha$ to $90$, $\cos$ would become $0$. Do you see why I think this? Look at the digram, isn't that reasonable to think? Similarly, $\cos(0)$ I would have said should equal $1$ (twice that of $\cos(45)$ )

While $\cos(0)$ does equal $1$, this does not check out: $$ cos(90) = -0.4$$

Just do not get that $0.4$? Could someone explain? That just makes no sense to me. None.

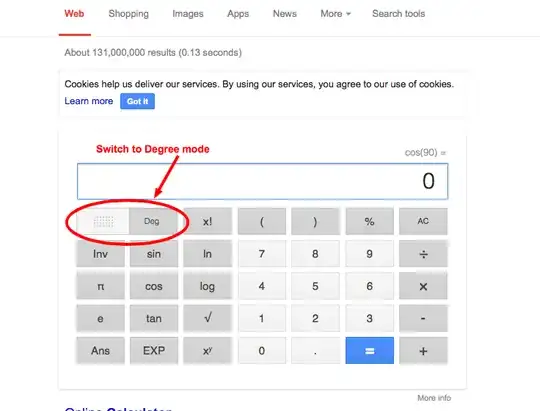
I'm using the google calculator and I would stress I have not touched maths for about $6$ years (ever since I left school!) so please lots of examples and words to explain!

$\cos 45° = \frac{1}{\sqrt{2}} \approx 0.707\dotsc$. But $\cos 45 \approx 0.52532$, the trigonometric functions take their arguments in radians in all programming languages I know. — Daniel Fischer, May 12 '14 at 22:40
Okay guys, I know it's fun to have questions that start with "I'm a graphical artist...", but I don't think a simple trig question really needs six upvotes. — Jack M, May 12 '14 at 22:55
@Jack, votes are independent. Do you think if somebody comes along and likes the question, they should refrain from voting on it just because too many other people have already done so? — , May 12 '14 at 23:16
@JackM Haha! I was not going to upvote this, until...you said it. — Cheeku, May 12 '14 at 23:49
It's a good question with a lot of effort put in. +1 from me. — friedo, May 12 '14 at 23:58
@JackM I disagree. I'm glad that a layperson in "industry" can use this site to get help. I think this should be encouraged and thus upvoted. — Brian Fitzpatrick, May 13 '14 at 00:01
It's a well-researched question, with a problem that many might have, with an answer that isn't trivial if you didn't instantly recognize it. +1 — lily, May 13 '14 at 01:42
Though lots of people have said that you're looking for radians, not degrees, it might not be obvious why radians are the sensible measure. Consider your diagram, and suppose the angle alpha is 45 degrees, which is pi/4 radians. That is the length of the fraction of the unit circle on your diagram from the x axis to the line. That is, if you consider the "curvy triangle" made from the x axis, the diagonal line and the curved side, then the sides are of length 1, 1 and alpha respectively. Radians are a very natural measure for this reason. — Eric Lippert, May 13 '14 at 02:27
I also want to remark that sine, cosine and tangent for corners less than 90 degrees are calculated using a right triangle (one with a corner of 90 degrees). Sine is the ratio between the opposite side and the longest side, cosine is the ratio between the adjoining side and the longest side, and tangent is the ratio between the opposite side and the adjoining side (in the picture, the longest side is always 1 unit, so the cosine is just the adjoining side). In such a context, a cosine of a 90° angle doesn't really make sense, since that's no longer a triangle, but a trapezoid. — Nzall, May 13 '14 at 07:22
Of course, in the context of a corner on a cirle, this can be different and my high school trigonometry didn't quite cover it. — Nzall, May 13 '14 at 07:22
It's more likely 40°. 45° is half of a right angle and it doesn't seem to be half. — Qwerty, May 13 '14 at 09:23
@Eric Lippert Thanks Eric! The fact that radians start from the x axis cleared everything up! So with radians, we're dealing with an imaginary circle with a diameter of 2, right? Judging from the fact that cos(0Pi) = 1 and cos(1Pi) = -1? — Starkers, May 13 '14 at 12:21
@Starkers That's correct, though it's usually more natural to think of it as having a radius of 1 rather than a diameter of 2; for this reason, it's called a "unit circle". — lily, May 13 '14 at 13:32
@IstvanChung Brilliant, I get all of this! I like this unit circle..right in the dead center of infinity. — Starkers, May 13 '14 at 13:57
Why didn't anyone comment that the cosine is not bouncing! 13 hours later NoAnswer provides a solution. — Captain Giraffe, May 13 '14 at 21:38
Re: why we really do want to measure things in radians, I think the best answer to this is in calculus rather than geometry. — , May 14 '14 at 08:03
@CaptainGiraffe he didn't ask for a solution to the bouncing ball problem, that was just background to the question that came later. — Paul, May 14 '14 at 14:16
I never realized why the tangent had that name until I saw this diagram. Wow! — B. Szonye, May 15 '14 at 01:38
@BraddSzonye You might also be interested then to know that "secant" means a line that cuts, and that $\sec(\alpha)$ is the distance from the origin to the upper tip of the vertical segment representing $\tan(\alpha)$, cutting through the circle. — 2'5 9'2, May 18 '14 at 07:53

score 117 · Accepted Answer · answered May 12 '14 at 22:41

117

The cosine function takes radians as its argument in most computational languages.

Indeed, $\cos 45^{\circ} = \sqrt{0.5}$, and $\cos 90^{\circ} = 0$. However, in math, for various reasons, we don't like working with degrees. We work with radians, where $2\pi\ \textrm{radians} = 360^{\circ}$.

In fact, $\cos 90\ \textrm{radians} \approx -0.44807$ and $\cos 45\ \textrm{radians} \approx 0.525$.

90 radians would be about 5156 degrees, or about 14.3 turns around the circle!

answered May 12 '14 at 22:41

Emily

36,334

9

Wow my fingers were all over the keyboard on this one. – Emily May 12 '14 at 22:43
4

So if we were to "rotate clockwise" through all the radians, we'd start at cos(0Pi) and end at cos(2Pi)? Which of course are the same thing, but do you see what I mean? – Starkers May 13 '14 at 12:24
Yes, Starkers.. – Almo May 13 '14 at 13:22
6

@Starkers Yep. In fact, suppose you rotate by $\alpha$. Then, rotating by $\alpha + 2\pi k$ for any integer $k$ gets you the same thing! Think about skateboarding or figure-skating... a 360 is one spin, a 720 is two spins, but you end up facing the same direction. Likewise, a 180 flips you backwards, and a 540 flips you backwards after doing one complete spin. – Emily May 13 '14 at 14:28
5

As it turns out, this "multi-valuedness" of the $\cos$ function (and likewise, the $\sin$ function), turns out to be exceptionally important in many branches of mathematics! – Emily May 13 '14 at 14:29
8

@Starkers - I'd like to point out that while cos(0π)=cos(2π), I'd like to point out that it goes counter-clockwise, not clockwise. For example, sin(π/2) = 1, not -1. – Xynariz May 13 '14 at 15:55
1

This is the exact moment when I love to bring up Tau, where Tau=2Pi. It helps in visualizing the circle as 1 turn, thus 1 Tau to go 360 degrees. So understanding that (Tau/4) is a quarter turn, or 90 degrees, a quarter way around, makes it clear that cos(Tau/4) is 0 given the image in the original question. Tau Manifesto – spex May 16 '14 at 18:35
6

Ugh.${}{}{}{}{}$ – Emily May 16 '14 at 18:42
For the difference between 0°, 360° and so on, imagine a screw with a dot on the head: the dot points to the same direction, but the screw is deeper in the hole for every turn. – glglgl May 17 '14 at 10:23
@glglgl shallower in the hole. CCW turns would loosen the screw. – Emily May 17 '14 at 14:08
@Arkamis If I rotate CCW on a right-hand thread, yes. If I am connecting a gas cylinder, I might (depending on the gas) have a left-hand thread. But otherwise, you are right. – glglgl May 17 '14 at 22:09
2

I am baffled by the number of votes this answer has. – Emily May 19 '14 at 23:03

Brian Fitzpatrick · Answer 2 · 2014-05-16T04:34:52.047

41

Your problem is with units. As mathematicians, we generally measure angles in radians not degrees. The conversion is $$ x\text{ degrees}=\frac{x}{180}\pi\text{ radians} $$ Most software generally takes the argument of trig functions as radians. Thus $\cos(45^\circ)$ is computed as $$ \cos(45^\circ)=\cos\left(\frac{45}{180}\pi\right)=\cos\left(\frac{\pi}{4}\right)=\frac{1}{\sqrt 2} $$ You are correct that $\cos(90^\circ)=0$, but when you input $\cos(90)$ into a calculator, the calculator reads $90$ in radians, not degrees. What you should input is $$ \cos(90^\circ)=\cos\left(\frac{90}{180}\pi\right)=\cos\left(\frac{\pi}{2}\right) $$ which will return as $0$.

For evidence, type cos(90) into google (here google interprets 90 in radians, not degrees). Compare by typing cos(90 degrees) into google.

To summarize, if you want to find the value of $\cos(x^\circ)$, type $$ \cos\left(\frac{x}{180}\pi\right) $$ into your calculator.

edited May 16 '14 at 04:34

answered May 12 '14 at 22:42

Brian Fitzpatrick

26,933

3

Bonus question: Trying with a randomly typed number such as 63.948, google calculator tells me that $\cos(63.948)$ and $\cos(63.948^\circ)$ are the same number (up to some rounding effects) - how come? – Hagen von Eitzen May 13 '14 at 06:46
3

@HagenvonEitzen For me? Well $63.948^\circ\approx 1.116\operatorname{rad}\approx 63.948-20\pi\operatorname{rad}$ – Brian Fitzpatrick May 13 '14 at 07:01
6

@HagenvonEitzen: There are an infinite number of such coincidences, actually. They're the points where cos(x)=cos(πx/180) – MSalters May 13 '14 at 15:35
2

@MSalters -- but are there a countable infinity? (Answer: yes. Proof is left to the interested reader.) – Michael Lorton May 15 '14 at 10:57
2

@Malvolio: Of course. Take the difference, there's a finite number of zeroes every 2 pi (at most 4), and there are countably many non-overlapping intervals of length 2 pi. – MSalters May 15 '14 at 13:20

score 26 · Answer 3 · edited Jun 12 '20 at 10:38

26

Your written question may be: Could somebody explain cos to an idiot please? I will not answer this, as it wouldn't be helping.

The question answered is more like: Why is cos not behaving like I expect it to? I won't answer this either, as it is already answered sufficiently. And it's probably a duplicate...

However I want to answer your intended question, at least as I anticipate it. For this I will concentrate on this part of your question:

However, I'm dabbling in WebGL (3D software for internet browsers) and trying to animate a bouncing ball.

Apparently we can use trigonometry to create nice smooth curves.

I anticipate your real question might be something like: How do I get a nice path to animate a bouncing ball?

The answer is: Not with trigonometric functions as they help you with circular movement, e.g. a ball fastened on a string whirling around a fixed point. You should try a parabolic path. The function y = x² is the easiest example for a parabel. But you probably want to set a starting point, swap and stretch it.

So instead of an explicit function for each point on the path you could use a simple iterative process:

Have a starting position (x,y), a starting speed (m,n) and some kind of gravity (g, ~10m/s² will look natural but that's something for advanced). For each iteration you update your position like this:

x := x + m
y := y + n

and your speed:

n := n - g

To make the ball bounce you invert the speed when it hits an obstacle, e.g. bouncing from the ground at level b:

if (y < b) then n := -n

This will provide a quite basic behaviour and needs some tuning and extensions, especially for natural motion, sharp borders of obstacles, decreasing bounce height, etc.

Note that I use := to resolve the problem that x = x + m would require m = 0 to be correct in a mathematical context. The "operator" := is meant as a redefinition to spare you an iteration index or parameter, i.e. x_i or x(i).

edited Jun 12 '20 at 10:38

Community

1

answered May 13 '14 at 09:42

NoAnswer

297

Trigonometry can be used to calculate the shape of the parabola. – user877329 May 17 '14 at 12:36
Test for if (y < b) after calculating y but before rendering at y. When y < b not only recalculate n but y as well before rendering. Otherwise the ball will fall through the floor (b) before it bounces. – candied_orange May 18 '14 at 12:01
@CandiedOrange: On math.stackexchange you're correct. However in practice for sufficiently small timesteps and/or low speed there's next to no difference. You'd want small timesteps anyway for a smooth animation. Without quite some additional effort you can either choose, if the ball dips slightly into the ground or bounces off before touching the ground. Choose your poison or go the extra length of introducing variable length timesteps and a collision detection that supports them. Oh, if you're doing the latter you can also start with integration over time. But OP had problems with cosine ... – NoAnswer May 26 '14 at 15:08
@user877329: As far as I remember, there are transformations to represent any function in terms of sine/cosine. So you are right in theory. However, I doubt the transformation will make y=x² any simpler. For an animation path y=x² is not a good representation, because you need some model of time. The iterative procedure I described is again really simple. It also provides a nice parabolic path, that can be of high precision due to low complexity for each time step. Feel free to provide an approach using sine/cosine that has any advantage over what I gave. – NoAnswer May 26 '14 at 15:26
@NoAnswer If you know the elevation angle, you will need sine and cosine to get the y and x components of the initial velocity, shaping the parabola. When the angle equals $\pi/2$ there will be no parabola. – user877329 May 26 '14 at 15:43
@user877329: Uhm, yes. You can apply sine and cosine to get starting values for m and n for a given elevation angle. But you can also just "guess" values for m, n and g and have a look. pi/2 is equivalent to m=0. It's still a parabolic movement but the parabel is "squashed" to a line. However, this is going far off-topic now. I just wanted the OP to know, he's wrong, if he assumes a ball naturally bounces along a circular path. And I anticipated his assumption by him writing "Apparently we can use trigonometry to create nice smooth curves.". – NoAnswer May 26 '14 at 16:34
@NoAnswer Even with very small amounts of time between frames, with an large enough initial height and a small enough ball it will completely disappear under the floor for one frame if you don't test before you render. This will be noticeable. – candied_orange May 28 '14 at 07:07
@CandiedOrange: You are referring to my first comment: However in practice for _sufficiently small_ timesteps and/or low speed there's next to no difference. With a large enough initial height (or an equivalent starting speed directed at the ground) your very small amounts of time between frames is not sufficiently small as the implicit definition is related to speed. True, I didn't define it, hence implicit. My actual point is: The ball either changes its vertical direction one frame before "touching the ground" (check before render) or one frame after (check after render)... – NoAnswer Jun 04 '14 at 16:30
... The solution is to go the extra length of introducing variable length timesteps and a collision detection that supports them. plus integration over time. Only then you can actually determine the point in time when the ball is "touching the ground". Otherwise you will always be "half a frame" too early or too late with changing the direction. – NoAnswer Jun 04 '14 at 16:40
@NoAnswer Yes you could. Or you could simply test before rendering so there's no chance the ball is ever rendered halfway through the floor. That's the frame that will look silly. If, for some reason, getting dead accurate height depictions for every frame is important than simply shift events in time until impact occurs at a rendered point in time. So long as it's just a ball bouncing off the floor that's enough. – candied_orange Jun 05 '14 at 06:27
@CandiedOrange My point is that it doesn't matter. There will always be something looking silly, either because the ball penetrates the ground or because it bounced off without touching the ground. Your proposal is valid but does not provide an objectively measurable benefit. You may have the last word, if you like. I can't state it any clearer than that. – NoAnswer Jun 05 '14 at 09:49
@NoAnswer The reason I'm claiming it matters is because not rendering the ball at exactly the moment of impact is the same thing a real film would do. It would simply appear as if impact happened between frames. This is noticeably better than showing the ball half way through the floor. I really don't care about the last word but I'd like to feel like I'm being understood. – candied_orange Jun 07 '14 at 14:08

score 15 · Answer 4 · answered May 12 '14 at 22:41

There are two common units of angle measurement: degrees, with $360$ degrees making one full circle, and radians, with $2\pi$ radians making one full circle.

Calculators can usually be switched from one "angular mode" to another. Your calculation of $\cos(90)$ comes from using a calculator in radians mode, while your angle is in degrees. (You're perfectly correct that the cosine of $90$ degrees is $0$.)

200_success · Answer 5 · 2014-05-14T13:00:09.073

You've made multiple errors in your question.

Let's set α to 45 (around where it appears to be in the diagram) and find the cosine value, thus giving us the green line.

cos(45) = 0.5

Fair enough. cos(α) / the green line is 0.5 units.

The green line is not 0.5 units.

The green line, red line, and the $x$ and $y$ axes form a square whose diagonal is 1 unit. By the Pythagorean Theorem,

$$ \begin{array}{} (\cos \alpha)^2 &+\quad (\sin \alpha)^2 &= 1^2 \\ (\cos \alpha)^2 &+\quad (\cos \alpha)^2 &= 1 \tag{green length = red length}\\ \end{array}\\ \cos \alpha = \cos 45^\circ = \frac{1}{\sqrt 2} \approx 0.707 $$

Therefore, the length of the green line is about 0.707.
Similarly, cos(0) I would have said should equal 1 (twice that of cos(45) )

While it is true that $\cos 0 = 1$, there is no justification for "twice that of cos(45)".
cos(90) = -0.4

Just do not get that. 0.4? Could someone explain? That just makes no sense to me. None.

I'm using the google calculator…

Google Calculator uses radians as the default unit for angles. The conversion between units is: $360^\circ = 2\pi\ \textrm{radians}$. Therefore, Google Calculator interpreted your request as

$$ \cos 90 = \cos \left(90 \cdot \frac{360^\circ}{2\pi}\right) \approx \cos 5156.62^\circ $$

To get the result you intended, you have to switch it to Degree mode before typing c90=

score 6 · Answer 6 · answered May 13 '14 at 04:38

Others have already explained that you were getting results from the calculator for radians and not degrees.

You can make the Google calculator (and most others) work in degrees as well. When you bring up the calculator, the upper left button will say "Rad" and have a blank button (slider) next to it. If you click the slider, you change the calculator to "Deg" (degrees) mode. Then hit AC to clear the calculator, and type in a new calculation right in the calculator answer window (not the google serach bar).

score 5 · Answer 7 · answered May 13 '14 at 19:14

Cosine and sine functions create smooth curves when plotted as a function of time. If you graph $$\cos\left(2\pi t\right)$$, where t is time in seconds, the ball will be start at height 1, drop to height 0 at 1/4 sec, bounce back up to 1 at 1/2 sec, 0 at 3/4 sec, 1 at 1 sec, and so on.

You can change the frequency by changing what is in the parentheses. For example, $$\cos\left(4\pi t\right)$$ will bounce twice as fast and $$\cos\left(\pi t\right)$$ will bounce half as fast.

If you multiply the whole function by a value it will change the height of the function. So $$4\cos\left(2\pi t\right)$$ will cause the ball to bounce four times as high.

Many oscillating things, like light and sound waves, follow this kind of trigonometric function. But a bouncing ball does not, so it might not look natural. Here's a site that gives the correct equation for a bouncing ball.

score 0 · Answer 8 · answered May 15 '14 at 15:01

I've looked over the answers so far, and I it very likely with all that 'accurate' information, you may well have the answer you need. If not, I can sympathise with your dilemma so if I may, I can make a few basic suggestions from my initial "experience" with Fourier Calculus. It can be confusing and may not address 'fundamental question':

Unfortunately, I just cannot see why.

As I get this, the emphasis is on "why"? In that spirit, I suggest that the issue is firstly that you may be a visually oriented person, I take my lead on that because you 'get' the diagram above. So you understand that the COSINE() function of an angle, is a ratio of two sides of any right-angle triangle: Adjacent and Hypotenuse.

Cosine

Related, geometrically, to the angle with the adjacent adjacent to the sloping side (hypotenuse).

If I can suggest the "lazy way" first; the fraction created from the ratio between these sides as the corner-angle, alpha, changes is-a *curve*in Euclidean space. So if you take a grid and plot sides: (x, y) at the centre for angle alpha ...

x = (Length of the Adjacent side)
y - (Length of the Hypotenuse side)

On an axis ... as you change the angle you will see a Cosine curve traced at the opposite point. Common tools and web graphics use this to make 'magical' sprials and stuff. As a boy I had a Spirograph ... it creates patters. ALL of these are based on the same rations from a circle/triangle. It is a kind of magic, just like the Greeks thought. Beauty may be truth.

Why? If you don't have a Spirograph - You can makes some cool substitutes.

Create a triangle shape with three flat lengths of wood.
You can ensure the triangle retains rectangle with a nail or tight screw.
Leave the other two sides - FREE to move.

When you attach a pen to the arms of this right-angle, and move the sides(arms); you will trace curves. Congratulations, they are cos or sin curves!

Once upon a time 'science' like Geometry included philosophy and 'manners' for conduct. We don't live in that world any longer, do we? The aim of Geometry is to consider every thing (material item) objectively in 3-Dimensional space. At that time, 3,00 years ago Science was a kind of magic.

The "Smooth CURVES" you asked about, were considered part of the bounty or reward to those of enquiring minds. Recall that is is like, 2,000 years before Picasso -- Euclid had abstract art. And pretty cool stuff too!

......

score -1 · Answer 9 · answered May 18 '14 at 11:28

-1

Wrong unit. You talk about deg, while the function obviously expects rad, which gives -0.4.

answered May 18 '14 at 11:28

user151773

1

Why is $\cos (90)=-0.4$ in WebGL?

9 Answers9

Linked