Function $f: \mathbb{R} \to \mathbb{R}$ that takes each value in $\mathbb{R}$ three times

Question

Does there exist a function $f: \mathbb{R} \to \mathbb{R}$ that takes each value in $\mathbb{R}$ three times? If not, how could I prove that such a function does not exist?

Answer 1

Here's a continuous solution:

$$ f(x) = \begin{cases} 4x-3\lfloor x\rfloor & \text{when $\lfloor x\rfloor$ is even} \\ 3\lfloor x\rfloor + 3 - 2x & \text{when $\lfloor x \rfloor$ is odd} \end{cases} $$

This takes on the values $0,4,2,6,4,8,6,10,8,\ldots$ at integer $x$ and interpolates linearly between them.

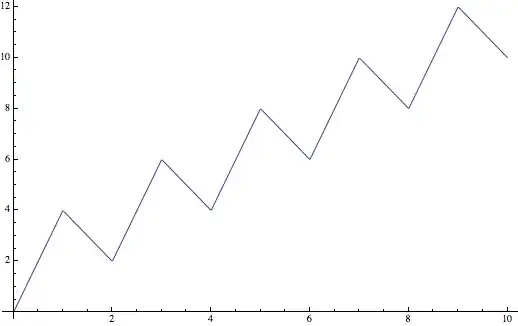
Any even number $2m$ is hit at $f(2m)$ (a local minimum), $f(2m-\frac32)$ (the middle of an increasing line segment), and $f(2m-3)$ (a local maximum). All other numbers are hit by a point in an increasing line segment, then a decreasing one, and finally another increasing one.

---

A smoother function with the same overall shape would be $g(x)=ax+\sin x$, except the coefficient $a$ has to be just right in order to get the local maxima and minima to coincide, and I'm too lazy to figure out what it should be.

Answer 2

I am exporting the answer I gave to a closed question.

$$f(x)=2\left\lfloor\frac{x}{3\pi}\right\rfloor-\cos\left(3\pi\left\{\frac{x}{3\pi}\right\}\right)\tag{1}$$ is a differentiable function that attains any real value in exaclty three points, whose graphics is the following one:

$\hskip2in$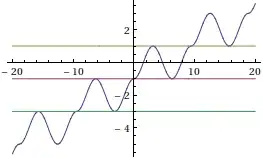

If in $(1)$ you replace "$3$" with the positive odd integer $2m+1$, you get a function that attains any real value in exactly $2m+1$ points. You can also take:

$$f(x) = T_{2m+1}\left(x-2\left\lceil\frac{x-1}{2}\right\rceil\right)+2\left\lceil\frac{x-1}{2}\right\rceil,$$

where $T_{2m+1}$ is the $(2m+1)$-th Chebyshev polynomial of the first kind. This is a $C^1(\mathbb{R})$ function, too.

Answer 3

Continuity works :

$$ f(x) = \left\{ \begin{array}{ll} 3(x-k)+k & 0\le x-k\le \frac{1}3 \\ −3(x−k)+2+k & \frac{1}{3}\le x-k\le \frac{2}3 \\3(x−k)−2+k &\frac{2}{3}\le x-k\le 1 \end{array} \right. $$

In fact one can prove the following statement : There exists a continuous function that takes all the values ​​of its image exactly $n$ times if and only if $n$ is odd.

Answer 4

Yes, in fact there is a very general way to construct functions like this. For example, essentially the same proof works for any $n$ instead of just $3$.

It suffices to note that $\mathbb R$ and $\mathbb R\times \{0,1,2\}$ have the same cardinality. To see this, note that we have an obvious injection $\mathbb R\to \mathbb R\times \{0,1,2\}$, and we can define an injection the other way by $$f(x,y)=\begin{cases} \arctan x\ &\text{if } y = 0\\ \arctan x + \pi &\text{if } y = 1\\ \arctan x + 2\pi &\text{if } y = 2 \end{cases}$$ thus by Bernstein-Schroeder there exists some bijection $g:\mathbb R\to \mathbb R\times \{0,1,2\}$. Now let $h(x)$ be the first component of $g(x)$.

Answer 5

If you can construct a bijection $\varphi:[0,1)\to(0,1)$, then you can construct bijections $f:(-\infty,0)\to(-\infty,\infty),\ g:[0,1)\to(-\infty,\infty)$, and $h:[1,\infty)\to(-\infty,\infty)$, and take their union.

Namely, let $f(x)=\log(-x),\ g(x)=\tan(\pi(\varphi(x)-\frac12)),\ h(x)=g(\frac2{\pi}\arctan(x-1))$.

Answer 6

Here's a continuous, non-piecewise function that does it, and it's very simple too. Consider $$f(x) = \sin(x) + \frac{2x}{3\pi} \text{.}$$

Answer 7

$\text{cotan}(\frac{3\pi}{1+e^{-x}})$ will do. Here is the plot of the function: