33

What is the relationship between cubic B-splines and cubic splines?

user105627
  • 565
  • Possible duplicate: http://math.stackexchange.com/questions/293542/cubic-spline-verses-cubic-b-splines – bubba Mar 05 '14 at 02:12

3 Answers3

46

A cubic spline is just a string of cubic pieces joined together so that (usually) the joins are smooth. The argument values at which the joins occur are called "knots", and the collection of knots is called a "knot sequence" or "knot vector".

Let's take the knot sequence to be fixed, for a while. Then the set of all cubic splines (with these given knots) forms a vector space, and it turns out that some things called b-spline basis functions form a basis for this vector space. If you don't know anything about vector spaces, this just means that you can write any spline uniquely as a linear combination of these basis functions. When you write a spline curve as a linear combination of b-spline basis functions in this way, it's called a "b-spline". So, b-splines are not a new type of spline, they are simply a different way of expressing any existing spline, in much the same way that "XVI" is a different way of expressing the number sixteen. And the important point is that any piecewise polynomial (i.e. any spline) can be written as a b-spline.

The functions $B_0$, $B_1$, $B_2$, $B_3$ that you described are the pieces that are used to form basis functions in the special case of cubic splines with uniform knots. The word "uniform" just means that the knots are equally spaced, so, usually, they are taken to be integers ... 0,1,2,3,4,... The nice thing about uniform knots is that all the resulting basis functions have identical shape, so any one of them can be obtained just by translating one primary one (moving it to the left or right). And, because the knot spacing is so simple, it's easy to write down explicit formulas for these uniform basis functions.

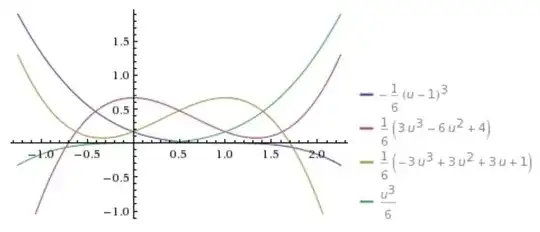
This picture shows the graphs of your four functions: enter image description here

Then, here, we focus on the interval $[0,1]$. The functions are labelled $a$, $b$, $c$, $d$, instead of $B_0$, $B_1$, $B_2$, $B_3$. \begin{align*} a(u) &= \tfrac16 u^3 \\ b(u) &= \tfrac16 \left( 1 + 3u + 3u^2 - 3u^3 \right) \\ c(u) &= \tfrac16 \left( 4 - 6u^2 + 3u^3 \right) \\ d(u) &= \tfrac16 \left( 1 - u\right)^3 \end{align*}

enter image description here

To form any basis function, you shift these pieces and glue them together, as shown here:

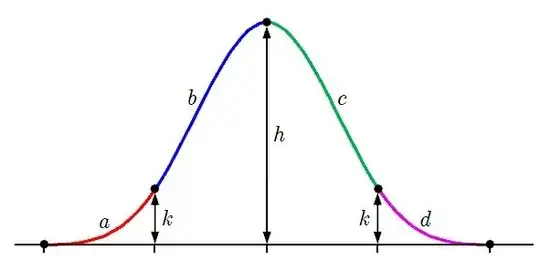
enter image description here

A few simple calculations, using continuity, show that in fact $h=2/3$ and $k=1/6$. This composite curve is $C_2$. As I mentioned above, you can get any other (uniform) basis function by shifting this one to the right or left.

If the knots are not uniform, then the basis functions are much more complex, and people don't usually write out closed-form formulas for them. Instead, they are generated recursively by the deBoor-Cox algorithm, starting with degree zero and working upwards to higher degrees.

For more info, look here, especially at "unit 6", or here, or here.

bubba
  • 44,617
  • What you said it makes perfect sense to me but I still have a small gap. The cubic spline function can be written as the linear combination of the B_ks: $S_3(x)=\sum_k^N \phi_k B_k(x)$ where $B_ks$ are the basic functions that I described before and $\phi_k$ the control points. – user105627 Mar 05 '14 at 15:31
  • I will consider a 1D problem. If the control points are known: i.e. $x_0=1,x_1=2,x_2=3,x_3=4$ and $\phi_0=0,\phi_1=2,\phi_2=4,\phi=2$. When I used my basis function I ended up with this $S_3(x)=0 \times (1-x^3)/6+2 \times (3x^3-6x^2+4)/6+4 \times (-3x^3+3x^2+3x_1)+2 \times x^3/6$. I expected that when I substitute x=1 i.e. S(1) it will give me $0$ because the $\phi_0=0$. Instead of zero I got 13/6. It happens to know how can I use the basis functions? – user105627 Mar 05 '14 at 15:32
  • You are using knots 1,2,3,4. This means you are focussed on the interval $[2,3]$. But your "B" functions are designed for use on the interval $[0,1]$. You have to shift them to the right to get basis functions for $[2,3]$. See pictures. – bubba Mar 06 '14 at 00:31
  • How did you recognised that the "B" functions are designed for use on the interval [0,1]? I have to focus on the interval [2,3] because 1 and 4 are the boundaries? – user105627 Mar 06 '14 at 11:17
  • By graphing them. Look at the first graph in my answer. The nice pattern I want occurs on the interval $[0,1]$. I guess you have to know what you're looking for -- the shapes shown – bubba Mar 06 '14 at 12:05
  • OK I just wanted to confirm that I understand well. I didn't came across with this area before and I have a lot of gabs. If I have an interval 1,2,3,4,5,6 for instance I have to focus on [3,4] and [4,5] I am trying to understand the logic. I read the the links that you suggested me but in practise it's easier to understand something. – user105627 Mar 06 '14 at 12:14
  • If you need to work on some interval $[a,b]$ between two consecutive knots $a$ and $b$, then you need two knots to the left of $a$ and two knots to the right of $b$. In general, a b-spline basis function of degree $m$ requires $2m$ knot values to construct it. Look at the deBoor-Cox recurrence. But it's easier if you're using uniform knots -- you can just take a fixed set of basis functions and shift them left or right. – bubba Mar 06 '14 at 13:33
  • In the my case I had consider the interval 1,2,3,4 these are uniform knots. But the basis functions I described before are for the interval [0,1] $a=(1-u)^3/6, b=(3u^3-6u^2+4)/6, c=(-3u^3+3u^2_3u_1)/6,d=u^3/6$. For the interval [2,3] the one that I have to focus I have to shift them right by 2? i.e. $a=\frac{(1-u)^3+2}{6}, b=\frac{(3u^3-6u^2+4)+2}{6}, c=\frac{(-3u^3+3u^2_3u_1)+2}{6},d=\frac{u^3+2}{6}$. Is that correct? – user105627 Mar 06 '14 at 15:27
  • 1
    No, you should avoid that (see end). Those basis functions are a basis not of the spline space, but of the space of polynomials of degree 3 or less. When computing a spline, you construct and solve a large linear system for the first or second derivatives of the spline in the knots. Then for each interval you have a pair of values at each end that can be uniquely transcribed into coefficients of a cubic polynomial in any basis. What is special about your basis? To plot or compute values, use a local parametrization with the interval $[0,1]$ for each interval. One procedure for many intervals. – Lutz Lehmann Mar 06 '14 at 18:55
  • Different people use the the term "spline" differently. To some people (like me, and Carl deBoor), a spline is just a piecewise polynomial. To others, it's a piecewise polynomial with maximum continuity (i.e. a $C_2$ function in the case of cubics). – bubba Mar 07 '14 at 01:41
  • Regarding the term "spline", see this question: http://math.stackexchange.com/questions/452844/spline-interpolation-versus-polynomial-interpolation/453833#453833 – bubba Mar 07 '14 at 01:46
  • It seems to me that this discussion is not converging. I suggest you ask a new question that tells us what you're trying to do. The original "what is the difference" question was answered long ago. It's hard to provide good advice without a better description of the problem. – bubba Mar 07 '14 at 01:48
  • One last try ... To get the basis functions for the interval $[2,3]$, you have to take your original ones $B_i$, which work on $[0,1]$, and shift them 2 units to the right. So, your shifted basis functions are $\tilde{B}_i(u) = B_i(u-2)$. So, for example, the first basis function for $[2,3]$ is $\tilde{B}_0(u) = B_0(u-2) = (1 - (u-2))^3 = (3-u)^3$. And so on. – bubba Mar 07 '14 at 04:36
  • There is something that I asked you before about the interval. How did you understand that I have to focus on interval [2,3]? If I use knots 1,2,3,4,5,6 for instance on which interval I have to focus? – user105627 Mar 07 '14 at 10:29
  • Ask another question, please, and provide a good description of what you want to do. I think I have answered your first question. – bubba Mar 07 '14 at 11:42
11

Splines as interpolating curves of minimal curvature

For curves with moderate curvature, the second derivative is a good proxy for the real curvature (inverse of the curvature radius).

A spline is the minimizer of the variational problem to interpolate a given set of points while minimizing the second derivative: $$ y=\mathop{\arg\min}_{u\in H^2([a,b])}\int_a^b \|u''(x)\|_2^2\,dx\qquad\text{ s.t.}\qquad \begin{split} u(x_k)=x_k,\quad k=1,2,...,n\\a\le x_1<x_2<...<x_n\le b \end{split} $$ The solution is

  1. piecewise cubic on intervals $[x_i,x_{i+1}]$,
  2. linear on $[a,x_1]$ and $[x_n,b]$,
  3. continuous up to the second derivative, and
  4. has the general formula $$ y(x)=a+bx+\sum_{k=1}^n c_k\, (x-x_k)_+^3 $$

B-Splines

The cubic B-spline (basis spline) centered at $x=0$ is

$$\beta_3(x)=\frac16\left[(x+2)_+^3-4\,(x+1)_+^3+6\,(x)_+^3-4\,(x-1)_+^3+(x-2)_+^3\right]$$

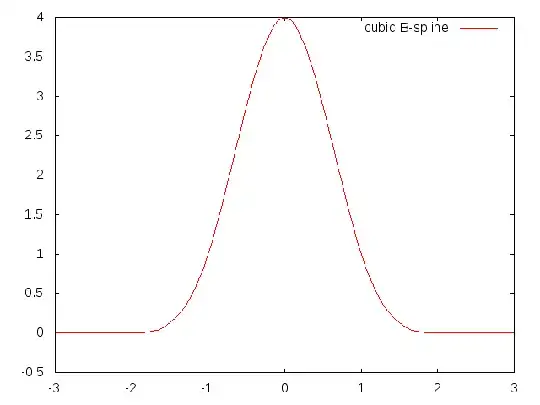
(graphic has wrong scaling, too high by a factor of 6) cubic B-spline centered at 0

which obviously invalidates that the function values at integers are only 0 and 1. But still it is a compactly supported, minimally so, spline function with nodes at the integers.

Locally, every cubic spline with integer nodes can be expressed as a linear combination $\sum_{k=m}^nc_k \beta_3(x-k)$ of B-splines.

Bezier curves

Bezier curves, sometimes called Bezier splines, have the formula $$ y(x)=(1-x)^3P_0+3(1-x)^2xC_0+3(1-x)x^2C_1+x^3P_1 $$ for $x\in[0,1]$.

In the general spline context, they can be used to express one segment of a spline. Not every concatenation of such segments results in a spline, the continuity of first and second derivatives must be ensured.

The nice property of Bezier curves is that they can be evaluated as convex combinations of convex combinations of... If $[A,B]_x=(1-x)A+xB$ then $$ y(x)=\Bigl[\bigl[\,[P_0,C_0]_x,[C_0,C_1]_x\,\bigr]_x,\,\bigl[\,[C_0,C_1]_x,[C_1,P_1]_x\,\bigr]_x\Bigr]_x $$

Other parametrizations of cubic segments

Your basis functions, also over the interval $[0,1]$, take the values $$ \begin{array}{|ccc|ccc|ccc|} B_k(x)&B'_k(x)&B''_k(x)&B_k(0)&B'_k(0)&B''_k(0)&B_k(1)&B'_k(1)&B''_k(1)\\ \hline \tfrac16(1-x)^3&-\tfrac12(1-x)^2&(1-x)&\tfrac16&-\tfrac12&1&0&0&0\\ \tfrac16(3x^3-6x^2+4)&\tfrac12(3x^2-4x)&(3x-2)&\tfrac23&0&-2&\tfrac16&-\tfrac12&1\\ \tfrac16(-3x^3+3x^2+3x+1)&\tfrac12(-3x^2+2x+1)&(-3x+1)&\tfrac16&\tfrac12&1&\tfrac23&0&-2\\ \tfrac16x^3&\tfrac12x^2&x&0&0&0&\tfrac16&\tfrac12&1 \end{array} $$ where one can see that values and derivatives at the $x=0$ match with those at $x=1$ in the next line. See update below for how to interpret this further.

Useful parametrizations are, in my opinion, $$ y(x)=(1-x)\,y(0)+x\,y(1)-\tfrac16x(1-x)(2-x)\,y''(0)-\tfrac16x(1-x)(1+x)\,y''(1) $$ and $$ y(x)=(1-x)^2(1+2x)\,y(0)+x^2(3-2x)\,y(1)+x(1-x)^2y'(0)-x^2(1-x)y'(1) $$

Update: Per bubbas answer above, I now see that the $B_k$ are the pieces of the cubic basis spline $β_3(x)$. So for $x\in[0,1]$, \begin{align} d(x)=B_0(x)&=\beta_3(x+1)=\tfrac16 \beta_3(-1-x)=\tfrac16 [(1-x)^3]\\ c(x)=B_1(x)&=\beta_3(x\quad\;\,)=\tfrac16 [(x+2)^3-4(x+1)^3-6x^3]=\tfrac16 [3x^3-6x^2+4]\\ b(x)=B_2(x)&=\beta_3(x-1)=\tfrac16 [(x+1)^3-4x^3]=\tfrac16 [-3x^3+3x^2+3x+1]\\ a(x)=B_3(x)&=\beta_3(x-2)=\tfrac16 [x^3]\\ \end{align}

Lutz Lehmann
  • 131,652
  • I found that the basis functions are: $B_0$ – user105627 Mar 05 '14 at 09:21
  • $B_0$ or $\beta_0$ usually refers to the rectangular box functions, either $1!!1_{[-1/2,1/2)}$ or $1!!1_{[0,1)}$. There is nothing cubic about them. Or did you mean the cubic B-spline centered about 0? – Lutz Lehmann Mar 05 '14 at 09:34
  • Thanks for your response. What do you mean with function values (...,0,0,1,0,0,..)? Cubic spline has any function value? Every cubic spline can be expressed as $S_3(u)= \sum_{k=0}^N a_k B_k(u)$ where $B_k(u)$ are B-splines? The basis functions of B-splines I found that are as follows: $B_0(u)=(1-u)^3/6$, $B_1(u)=(3u^£-6u^2+4)/6$, $B_2(u)=(-3u^3+3u^2+3u+1)/6$, $B_3(u)=u^3/6$. These basis functions are standard right? – user105627 Mar 05 '14 at 09:39
  • This I do not understand. I know of Bezier splines that are constructed with control points as $(1-x)^3P_0+3(1-x)^2xC_0+3(1-x)x^2C_1+x^3P_1$. Which in reality is just a way to describe a curve that is cubic in each component. A spline is defined by the way that these single cubic pieces are spliced together. B-splines are basis splines, $β0$ the box function and the others result from convolution, $β{k+1}=β_k*β_0$. So that $β_1$ is the witch hat,... – Lutz Lehmann Mar 05 '14 at 09:50
  • > This I do not understand. Take a uniform knot sequence like $\ldots, -2, -1, 0, 1, 2, 3, \ldots$, and form the corresponding b-spline basis functions of degree 3. By using the deBoor-Cox recurrence formula, for example, or "convolution", if you like. Among these basis functions, look at the four that are non-zero on the interval $[0,1]$. You will find that their values on $[0,1]$ are given by the four polynomials $B_0, B_1, B_2, B_3$. These polynomials are somewhat similar to the Bernstein polynomials used to construct Bezier curves, but not quite the same. – bubba Mar 07 '14 at 04:48
  • Basis functions in the sense of polynomial basis are arbitrary. $(1,x,x^2,x^3)$ is a basis. The ones now at the end of my answer, $((1-x)^2(1+2x),x^2(3-2x),x(1-x)^2,-x^2(1-x))$ and $((1-x),x,-\tfrac16x(1-x)(2-x),-\tfrac16x(1-x)(1+x))$ form a basis where the coefficients are the function values and first resp. second derivatives at the knots. So what favorable quality is there in the discussed basis functions? I gave their derivative values, there is not much special there. – Lutz Lehmann Mar 07 '14 at 06:24
  • 2
    What's special about the functions $B_0, B_1, B_2, B_3$ is that, when shifted and glued together as I showed in my pictures, they give a piecewise cubic function that is $C_2$. – bubba Mar 08 '14 at 01:23
  • Yes, I've seen that and added it to the end of my answer, it shows how it fits with the formula as sum of cubes. Also used it in the follow-up question, with reference to your answer here. – Lutz Lehmann Mar 08 '14 at 06:23
  • Lutzl what are the $\beta_3$ stands for in your answer? – user105627 Apr 07 '14 at 10:47
  • That is the cubic B-spline. $β_2$ would be the quadratic B-spline, $β_1$ the witch hat and $β_0$ the (centralized) box function. – Lutz Lehmann Apr 07 '14 at 12:06
  • 1
    The first derivative of $\beta_k(0)$ is incorrect. There is a negative sign missing in the front. – Luca Feb 26 '18 at 14:23
  • @Luca : Thank you, now it is also evident directly in the table that the functions match in values and first two derivatives at the interval ends. – Lutz Lehmann Feb 26 '18 at 16:05
  • "Bezier curves, sometimes called Bezier splines" Are they? Who calls them that? A single curve is a curve, maybe it can be considered a special case of a Bezier spline which just happens to consist of one curve. – cubuspl42 Mar 22 '25 at 09:23
  • "Not every concatenation of such segments results in a spline, the continuity of first and second derivatives must be ensured." Again, who assumes that? Fundamentally, composite splines just need to be C0 continuous (i.e. connect the sub-curves). C1 and C2 continuity is a possible additional requirement depending on the context. If this wasn't true, you couldn't call Bezier splines in 99% of computer graphics suites actual Bezier splines. – cubuspl42 Mar 22 '25 at 09:26
  • @cubuspl42: You could define splines as piecewise polynomial functions with certain continuity, or you could define them as the solution of a variational problem related to curvature. Then there is the distinction of approximating and interpolating splines, etc. Computer graphics mainly uses what is available in libraries and cares about theoretical content secondarily. – Lutz Lehmann Mar 22 '25 at 10:00
  • I understand your perspective. I'm just noting that the suggested constraints (at the theoretical level) exclude the vast majority of the theory's applications, which is counterintuitive. I understand that we could define splines in many ways, I'm just suggesting not to define them otherwise than it's commonly done, even in theoretical context. Spline on Wikipedia is defined as piecewise, so a single Bezier curve is at best a very special case spline. – cubuspl42 Mar 22 '25 at 11:08
0

This question, which was limited to cubic interpolation, can be generalized to arbitary degree of smoothness. That is, what is the relationship between B-splines and splines?

The difference is in methodology. The B-spline method adopts the perspective of function expansion using basis functions.

The basis functions used in B-splnes are with the builtin support for the boundary conditions between knots. So one does not need to worry about the boundary condtions once the knots are given and the corresponding basis functions are chosen.

In comparison, in conventional splines, users just use piecewise poloynomials and it is the user's responsibility to carefully choose the coefficients of the poloymonials to enforce the boundary conditions between knots. If you want to switch to a different degree of polynomials, you need to implement all the details that are related to the connection conditions between knots.

In summary, b-spline is a sysmatic method of doing spline interpolations, where you can easily switch to using whatever degree of smoothness you want.

Youjun Hu
  • 101