4

In numerical mathematics I have learnt about some interpolation methods, however today I've come across some sort of interpolation problem which I don't know how to solve or even work with:

Let $(x_i, y_i) \in \mathbb{R}^2, i=0, \dots, n$ and $y_i \geq 0$ for all $0 \leq i \leq n$. I want to find a function (preferably a polynomial of arbitrary degree) $f \geq 0$ such that $f(x_i) = y_i$ for all $0 \leq i \leq n$.

How would I approach the general case? Is there a general solution? I know of interpolation techniques considering derivatives (Hermite) and also know of spline-interpolation, but those don't really help. Thanks a lot in advance.

Huy
  • 6,867

1 Answers1

6

Positivity-preserving interpolation is hard, as searching for the italicized text will tell you. There are several things you could do, and the choice will depend on the practical context of your problem (not present in the question).

A cheap and dirty solution is to interpolate $(x_i,\sqrt{y_i})$ and square the interpolating function. If you interpolate with a polynomial, you'll have a nonnegative polynomial of twice the degree. The obvious drawback is that the squared function will have somewhat unnatural behavior in the regions where the interpolant was negative before squaring. Like on the right side of the graph here:

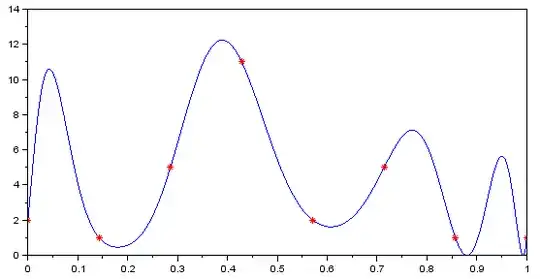
interpoly

Not to mention that interpolation by a high-degree polynomial is rarely desirable at all.

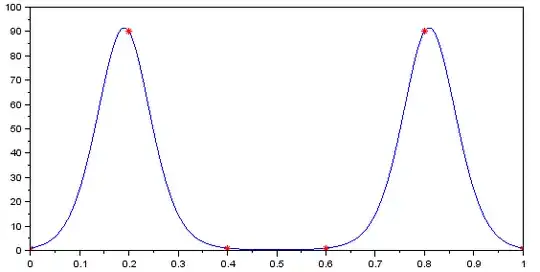
If you use spline interpolation (e.g., cubic spline), the behavior of interpolant is much better; it takes a bit of effort to produce an example where the interpolant becomes negative. Here I started with the values 1 90 1 1 90 1 at equally spaced points, interpolated their square roots with a natural cubic spline, and squared the spline:

spline

The bump around 0.5 is unpleasant. It would be better to use logarithm instead of square root, but of course then we don't have a piecewise polynomial as a result:

expoly

Still, in many cases the reason for data being positive is that it's naturally $\exp$ of something, so the above may be the best solution.

A completely different approach is to turn to approximation instead of interpolation. Using positive compactly supported functions such as $B$-splines, you can approximate positive data by a positive function.

A related question: Polynomial fitting where polynomial must be monotonically increasing

Related SE site: Computational Science

Community
  • 1
user127096
  • 9,993
  • I think the dirty solution will be best suited for my problem. I have values $y_i = 0$ which rules out taking the logarithm (or is there a solution for that issue?). However, if I am using Hermite interpolation (i.e. I want to interpolate derivatives as well), what values do I take for the derivatives? Simply the square roots? – Huy Feb 16 '14 at 14:33
  • @Huy Let's say $f$ is the function you want, and $g=\sqrt{f}$. Then $g'=f'/(2\sqrt{f})$, which means you should use $\dot y_i/(2\sqrt{y_i})$ as derivative values for interpolation. If $y_i=0$, then the corresponding derivative must be zero, otherwise there's no solution. – user127096 Feb 16 '14 at 15:48
  • I was thinking about using the logarithm method after all by simply adding a constant to my values (e.g. $y_i + 1$) and then taking the logarithm. However, when I then take the exponential of the resulting interpolating polynomial, is there a formula to find the constant I have to subtract in order to get back? In the examples I tried out I could not find any regularity and most importantly the constant $-1$ does not work. :-( – Huy Feb 16 '14 at 15:53
  • @Huy In general, what you do is apply some function $f$ to the $y$-values and then apply $f^{-1}$ to the interpolant. If you use $f(y)=\ln(y+1)$, then the inverse is $f^{-1}(y)=e^y -1 $. Problem is, this may be negative. If you use, say, $0.001$ instead of $1$, this may be less of a problem. – user127096 Feb 16 '14 at 17:39
  • Do you have any idea what the constant you use to subtract depends on in order for the resulting function to being non-negative? – Huy Feb 16 '14 at 22:27
  • @Huy It's possible there may not be any such constant. You see, if $f(y)=\ln(y+\epsilon)$ is used, then $0$ $y$-values are turned to $\ln \epsilon$. But the interpolant may dip below $\ln \epsilon$ (just as it dips below $0$ for nonnegative data), and you'll have same issue again. Suggestion: if your data contains some zero values at points $x_j$, introduce $p =\prod(x-x_j)^2$, interpolate $\ln(y_i/p(x_i))$ over $y_i\ne 0$, then use $p e^{g}$ where $g$ is the interpolant. This way, you "factor out" the zeros and deal with positive values only; then bring the zeros in. – user127096 Feb 16 '14 at 22:32
  • If the data is already positive everywhere, you can use https://docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.interpolate.PchipInterpolator.html#r57 – Jolle Nov 07 '19 at 15:46