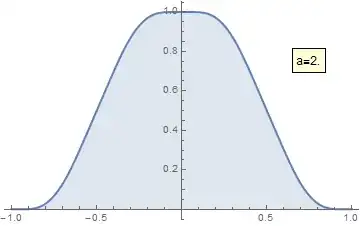
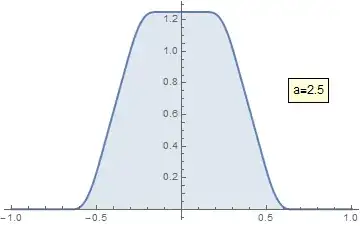
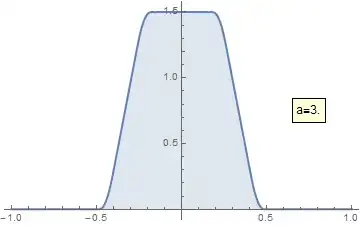
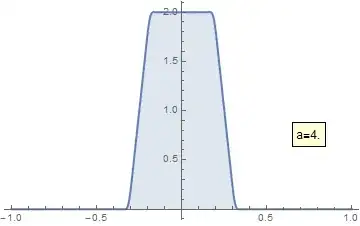
Calculate the infinite product $f_q(x):=\prod_{n=0}^\infty\frac{\sin(q^n x)}{q^n x}$, where $x$ is real and $0<q<1$.
In other words, $f_q$ must satisfy the functional equation $f_q(x)=f_q(qx)\operatorname{sinc}(x)$ with an initial condition $f_q(0)=1$, where $\operatorname{sinc}(x):=\frac{\sin(x)}{x}$.
Using the Euler's factorization of sinc one can rewrite $f_q(x)$ as a certain infinite product of $q$-Pochhammer symbols. Therefore I hope that $f_q$ can be expressed in terms of some hypergeometric functions. The Fourier transform of $f_q$ is a smooth function with compact support.