36

So the puzzle is like this:

An ant is out from its nest searching for food. It travels in a straight line from its nest. After this ant gets 40 ft away from the nest, suddenly a rain starts to pour and washes away all its scent trail. This ant has the strength of traveling 280 ft more then it will starve to death. Suppose this ant's nest is a huge wall and this ant can travel in a whatever curve it wants, how can this ant find its way back?

I interpret it as: I start at the origin. I know that there is a straight line with distance 40 ft to the origin, but I don't know the direction. In what parametric curve I will sure hit the line when the parameter $t$ is increasing, while the total arc length is less than or equal to 280 ft.

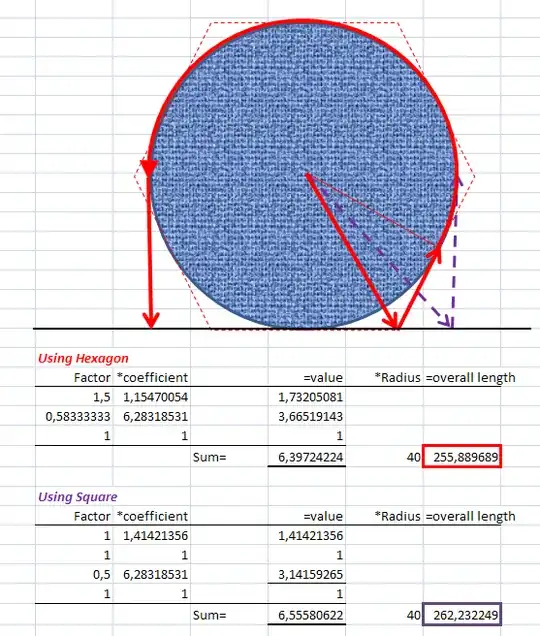
I asked a friend of mine who is a PhD in math, he told me this is a calculus of variation problem. I wonder if I could use basic calculus stuff to solve this puzzle (I have learned ODE as well). My hunch tells me that a spiral should be used as the path, yet I am not sure what kind of spiral to use here. Any hint shall be appreciated. Thanks dudes!

Clarification by dfeuer

As some people seem to be having trouble understanding the problem description, I'll add an equivalent one that should be clear:

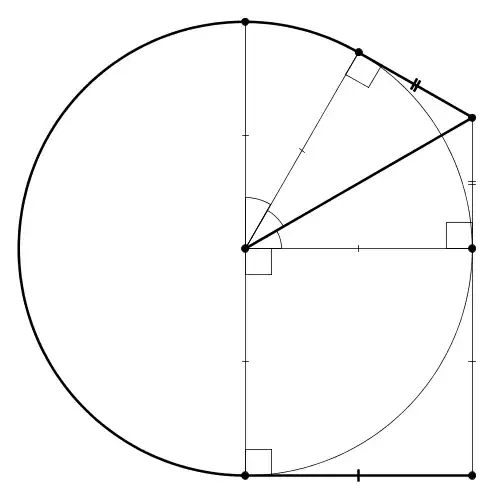
Starting in the center of a circle of radius 40 ft, draw a path with the shortest possible length that intersects every line that is tangent to the circle.

Constructor
  • 1,239
  • 8
  • 21
Tony Stark
  • 1,108
  • 9
  • 17
  • For all intents-and-purposes, the ant nest intersects tangentially anywhere on a circle of radius 40ft from the current position of the ant. Then the naive solution would be to walk out 40ft to an arbitrary point and then traverse the circumference of the circle. However, this uses at worst 40+2\cdot \pi 40 ft which slightly exceeds 280ft. Try to somehow cover more ground, perhaps by stepping outside the circle. – Alex R. Dec 12 '13 at 23:47
  • 1
    A lesson from the two current answers: while intuition may suggest spiraling out, you actually want to spend as much time as possible far from your starting position, so whatever you do, the first step should be to travel at lease 40ft in a straight line. – dfeuer Dec 13 '13 at 00:30
  • I'm so confused on what the question is asking. So the ant travels in some unknown direction for 40 ft in a straight line from the origin. Then what? – Shahar Dec 15 '13 at 01:20
  • @dfeuer Is it okay if I use a software to solve it or do I need to show steps? – Shahar Dec 15 '13 at 01:37
  • 1
    By the way, this is not a calculus-of-variations problem. – TonyK Dec 15 '13 at 21:42
  • What does the remark "the nest is a huge wall" mean/imply? What does it mean in this geometrical context? Does it possibly mean, that the ant can enter the wall-formed nest at any place, not only at the hole, where it left the nest? – Gottfried Helms Dec 15 '13 at 22:22

5 Answers5

36

Historical summary

It is the famous problem invented by R. Bellman in 1956 [1]. It is known as 'Lost in a Forest Problem':

What is the best path to follow in order to escape a forest of known shape and dimensions?

The subproblem for the half-plane forest with known distance from the boundary was solved by J. R. Isbell in 1957 [2]. He described the path with the length

$$\left(\sqrt{3}+\frac{7\pi}{6}+1\right)d$$

where $d$ is the distance from the boundary of the forest. He gave the proof in outline that his path had minimal length. The complete and detailed proof was given by H. Joris in 1980 [3]. The consideration about this problem can also be found in the book [4].

The overview of the results on the general problem up to 2004 can be found in [5].

Isbell's path

The form of the shortest path:

The shortest path

As @Will Nelson wrote the shortest path consists of the 3 line segments with lengths $\frac{2}{\sqrt{3}}d$, $\frac{1}{\sqrt{3}}d$ and $d$ and the arc of the circle with radius $d$ which subtends the angle $\frac{7\pi}{6}$. The total length of the path is

$$L_{\min}(d)=\frac{2}{\sqrt{3}}d+\frac{1}{\sqrt{3}}d+\frac{7\pi}{6}d+d=\left(\sqrt{3}+\frac{7\pi}{6}+1\right)d\approx 6.397d$$

In our case $d=40$ so $L_{\min}\approx 255.890<280$. The ant can survive!

References

  1. R. Bellman, Minimization Problem, Bull. Amer. Math. Soc. 62 (1956) p. 270. [Available online at the AMS BAMS archive, free of charge.]

  2. J. R. Isbell, An optimal search pattern, Naval Res. Logist. Quart. 4 (1957) pp. 357-359. [Available online at Wiley Online Library, 35$ cost.]

  3. H. Joris, Le chasseur perdu dans la foret, Elem. Math. 35 (1980) pp. 1-14. [Available online at the site of École polytechnique fédérale de Lausanne, free of charge.]

  4. Z. A. Melzak, Companion to Concrete Mathematics: Mathematical Techniques and Various Applications, Wiley, New York, 1973, pp. 150-153. [I couldn't find this book online. According to @Barry Cipra Google Books let some users see a big chunk of this book with relevant pages.]

  5. S. R. Finch and J. E. Wetzel, Lost in a Forest, American Mathematical Monthly 111 (2004) pp. 645-654. [Available online at the site of Mathematical Association of America, free of charge.]

Update: Some references were added.

Constructor
  • 1,239
  • 8
  • 21
  • I am interested in the optimality proof, will need to visit the local math. library tomorrow... – copper.hat Dec 15 '13 at 19:19
  • @copper.hat Unfortunately I couldn't find the original Bellman article in the Internet, only the later works of other authors and the review papers. Should I add references to some papers reviewing results received on this problem? – Constructor Dec 15 '13 at 19:28
  • The references you gave look sufficient to me... – copper.hat Dec 15 '13 at 20:12
  • @copper.hat I've added one overview paper. – Constructor Dec 15 '13 at 21:50
  • @copper.hat It looks like that original Isbell's paper doesn't contain the rigorous proof of the minimality. I've added the reference to the article where possibly can be found the complete proof, but sadly it is in French... – Constructor Dec 16 '13 at 19:17
  • Thanks! I haven't had a chance to go to the library yet. – copper.hat Dec 16 '13 at 19:19
  • @copper.hat It's a pity. I downloaded Isbell's article but I haven't understood his reasoning yet with my bad English. – Constructor Dec 16 '13 at 19:36
  • I found that googling on "melzak sailing curve" I could click through to a books.google.com copy of the relevant pages of the Melzak book. – Barry Cipra Dec 16 '13 at 19:36
  • @BarryCipra There is no electronic version of this book at books.google.com (or it is not available in my country). There is one at the top of google search results but I think I can't give such links here. And thank you very much for your link to the original Bellman problem definition! – Constructor Dec 16 '13 at 19:52
  • @Constructor, Google Books does seem to give different results to different people. It let me see a big chunk of the Melzak book, but another friend just now reported only being able to see pages 152 and 153. Sorry about that! But I'm glad I was able to help with the Bellman reference. – Barry Cipra Dec 16 '13 at 20:19
  • @copper.hat, From the Finch and Wetzel article, "In an important 1980 article, Joris supplied a complete and detailed proof [that Isbell's solution is optimal]". It sounds like Isbell did not give a complete proof, if that is what you are looking for. – Will Nelson Dec 16 '13 at 21:47
  • @WillNelson Isbell wrotes in his article: "Proof in outline, supposing a smooth solution exists." And "To convert this sketch into a rigorous proof is a routine exercise." So possibly you are right but Finch also claimed that Joris only rediscovered Isbell's solution. – Constructor Dec 16 '13 at 21:52
  • "The ant can survive!" .... iff it knows math. If so, we need that ant for our society. – Conor O'Brien May 08 '15 at 02:44
17

Rescale so that radius $R=1$. Assume the starting point (the center of the circle) is at $(0,0)$. Unless I've made a calculation error (I don't think so), the minimum is achieved with the following path:

  • Straight line from $(0,0)$ to $\left(\frac{\sqrt{3}}{3},-1\right)$.

  • Straight line from $\left(\frac{\sqrt{3}}{3},-1\right)$ to $\left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right)$.

  • Follow the circular arc counterclockwise about center $(0,0)$ from $\left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right)$ to $(-1,0)$.

  • Straight line from $(-1,0)$ to $(-1,-1)$.

The length of each of these subpaths is $\frac{2}{3}\sqrt{3}$, $\frac{1}{3}\sqrt{3}$, $\frac{7}{6}\pi$, and $1$. The total length is $$ \frac{7}{6}\pi + \sqrt{3} + 1 $$ or for R=40, $$ 40\left(\frac{7}{6}\pi + \sqrt{3} + 1\right) \approx 255.89. $$

I'll try to sketch a proof of this when I get a chance.

UPDATE: I'll begin to sketch a proof. Consider the unit circle $C$ centered at the origin in $\mathbb{R}^2$. Consider the line $l$ tangent to $C$ defined by $y=-1$. Fix two points $(x_+,-1)$ and $(x_-,-1)$ on $l$ such that $x_+\ge 0$ and $x_-\le 0$. Suppose $\Gamma$ is a path from $(x_+,-)$ to $(x_-,-1)$ such that the convex hull of $\Gamma$ includes $C$. Let $\Gamma'$ be any path from $(0,0)$ to $(x_+,-1)$ and then along $\Gamma$ to $(x_-,-1)$. Observe that $\Gamma'$ is an admissible solution to the problem, i.e., all tangent lines of $C$ intersect $\Gamma'$.

It turns out that the optimal solution to the problem must be such a path $\Gamma'$. That's the hard part of the proof, but it's intuitively quite clear if you think about it. And it's not hard to find the minimum length $\Gamma'$. To do so, fix $x_-\le 0$ and $x_+\ge 0$, then solve for the minimum length $\Gamma'$ with these values for $x_-$ and $x_+$. Then vary $x_-$ and $x_+$ to solve for the minimum length path overall. The minimum length $\Gamma'$ for fixed $x_-$ and $x_+$ is easy to find.

More details when I get a chance.

Will Nelson
  • 5,241
4

The envelope of the walls sweeps out a circle of radius $40$. Here's one possible method to find the wall (i.e. a path which intersects every tangent of the circle). From the origin, walk to $(0,40)$. Now walk counter-clockwise around the circle three-quarters of the way to $(40,0)$. Now walk vertically upwards to $(40,40)$. All in all you've travelled $40 + \frac{3}{2}\pi 40 + 40 \approx 268.5$ ft.

EuYu
  • 42,696
4

This is only a partial proof and it is intended only as an illustration of my comment to @copper.hat - a full proof seems already be given the other answer...

I'm not sure with the second part: The second part is, that we assume , the minimal path ends with a path walking on the circumference of the circle and finally on the vertical line down to the horizontal "wall-shaped nest"; this means the upper half circumference ( $p_4=r \cdot \pi$ ) and one radius ( $p_5 = r \cdot 1$ ) are assumed to be the minimal trailing path after the leading part has been done and thus is fixed to the length $p_4+p_5 = r \cdot (\pi+1)$ where $r=40$ is the radius.

The initial part of the path is then the variable part of the problem.
The ant has to go down to the wall with some angle $\varphi$ which is the first part of the path ( $=p_1$ ) , then it has to go back to the circumference ( second part $p_2$ ) , and walk on the circumference to the position $\pi/2$ on the circumference which is the end of the first quadrant (third part $p_3$ ).

  1. Obviously that part on the circumference is $p_3=r\cdot (\pi/2-2\varphi)$
  2. The part $p_1$ depends on the angle $\varphi$: $p_1 = r \cdot {1 \over\cos(\varphi)}$ and
  3. the part $p_2$ is $ p_2 = p_1 \cdot \sin(\varphi)$

So th variable part of the ant's path is $f(\varphi) = p_1 + p_2 + p_3 = r\cdot \left({1+\sin{\varphi}\over \cos\varphi} + \pi/2 - 2 \varphi \right) $ and for this a minimizing expression can be given: $ {d \over d \varphi} f(\varphi) = r \cdot \left({\sin^2 \varphi+\sin \varphi\over \cos^2 \varphi}-1\right) $ and the solution occurs indeed as $\varphi = 2 \pi/12 = 30°$ which is the half angle of the hexagon.

However, this is not yet the full proof; perhaps there is a somehow fractal path crossing the circumference to the inside of the circle, do some shortcut there and proceed - it must be shown, that there is indeed no shorter path for this part.

instructive picture

Constructor
  • 1,239
  • 8
  • 21
Gottfried Helms
  • 35,815
3

Here is a slightly shorter solution:

enter image description here

$40(\sqrt{2}+1 + \pi +1) \approx 262.2$.

copper.hat
  • 178,207
  • 2
    Is this optimal? An optimality proof of any solution will buy a small bounty. – dfeuer Dec 13 '13 at 00:33
  • @dfeuer: A good question. I am having a little difficult characterising solutions in a convenient way. – copper.hat Dec 13 '13 at 00:34
  • @dfeuer: So far I have not been able to show that there is a minimum. – copper.hat Dec 14 '13 at 19:38
  • There's a sort of lightning rod effect of points outside the circle, where knowing that the path reaches that point implies that if you draw the tangents from that point, the path intersects all the tangents that touch the circle between the points where those tangents do. I believe this constrains the shapes the path can take outside the circle, but I'm not sure just how. – dfeuer Dec 14 '13 at 21:37
  • @dfeuer: Assuming there is an optimizing solution, it must be rotation invariant (around the starting point), so the solution as such is not unique. I suspect that the path to showing that a minimizer exists will lead to a useful characterization. – copper.hat Dec 15 '13 at 00:54
  • It improves to the best solution (as given above) if you consider to take an hexagon instead of a square as reference-contour. – Gottfried Helms Dec 16 '13 at 01:04
  • @GottfriedHelms: Intriguing observation. – copper.hat Dec 16 '13 at 01:09
  • ![instructive picture][1] [1]: https://i.sstatic.net/Ygs15.png – Gottfried Helms Dec 16 '13 at 02:24
  • @GottfriedHelms: Nice picture! – copper.hat Dec 16 '13 at 02:58
  • At the question of a formula for the minimum: a provisorical assumption of a general minimal path could be, that the final part of the optimal path is on the boundary of the circle from the first to the third quadrant and then the vertical one-radius long line.
    For the first part, the length of the line from the center, by some angle down to the horizontal tangent, back to the circle and then the remaining tour on the circle to the end of the first quadrant a minimizing formula depending on the angle can be formulated. - But then a second proof is needed to justify the basic assumption...     – Gottfried Helms Dec 16 '13 at 07:45