There is a very rich theory addressing this problem, mainly developed by statistical physicists during the second half of the XX$^\text{th}$ century, known as percolation theory.
The main class of problems with which this theory is concerned can be stated like so:
Suppose a lattice consisting of many labelled sites interconnected in some specified order. Given that each site is independently occupied with independent probability $P$, what are the statistical properties of connected clusters?
Connected clusters are defined as sets of occupied sites which can be reached from one another by following the paths allowed by the lattice.
Example of lattices:
1-D percolation
This type of lattice consists of an infinite series of sites on the line.
$$...-\circ-\circ-\circ-\circ-\circ-\circ-\circ-\circ-\circ-\circ-\circ-\circ-\circ-\circ-\circ-\circ- ...$$
And after a realization of the experiment, with say $P=0.3$.
$$...-\circ-\bullet-\circ-\bullet-\circ-\circ-\circ-\circ-\circ-\circ-\circ-\circ-\bullet-\bullet-\circ-\circ- ...$$
Where I used the $\bullet$ symbol to represent occupied sites (probability $P$), and $\circ$ for unoccupied sites $(1-P)$.
Note that periodic boundaries are often assumed to simplify mathematical treatment.
Percolation on Cayley trees (Bethe lattice)
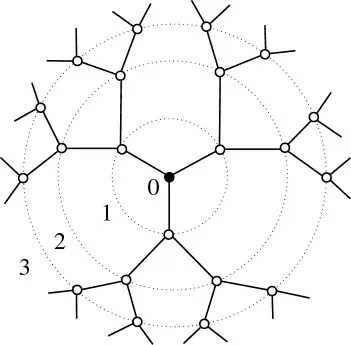
Every site has exactly $z$ neighbours in this type of lattice. The above is the Cayley tree for $z=3$
Some definitions:
Let me define the concept of spanning cluster: For a finite lattice, a spanning cluster is defined as a cluster that touches opposition boundaries of the grid.
We will also need to define the cluster size distribution. This is pretty self-explanatory: it is the distribution of cluster sizes, where the size of a cluster is defined as the number of connected occupied sites (disjoint from other clusters). I will use the notation $n(s;P)$.
A first answer
The 2 above lattices are amendable to an exact analytical solution because a walker on such grid can never loop back. Building on this observation, we can easily see that for a 1-d lattice of $L$ sites, the probability that a spanning cluster path exists is $P^L$. For the Bethe lattice, the question is already not as clear cut because one has to specify how it is cut.
This illustrates just how hard of a problem it is. Say there is no further site on the above image. We have to compute everything explicitly. Possible path could consist of going from level 3 to level 2 back to level 3 immediately. One could also go down as far as level 1 and backup, or through the central node. The problem is already somehow ill defined.
We can however make some statistical statements for the large sizes.
For example (and this is where the name derives from), it has been observed that over some critical threshold $P_c$, a giant component appears. That is, a cluster that occupies a finite fraction of an infinite lattice. On the line, $P_C$ is equal to 1, obviously. But on the Cayley tree, it is equal to $(z-1)^{-1}$. The probability that a given site is part of the giant cluster is then $$p_\infty=p\left[1-\left[1-2\frac{p(z-1)-1}{p(z-1)(z-2)}\right]^z\right]$$
We can also study the distribution of cluster sizes, as defined above. On the line, one finds that it is
$$n(s;P)=p^s(1-p)^2$$
since each finite cluster must be bounded by 2 occupied sites.
Now, for your question:
2-D lattice
\begin{align}
\begin{matrix}
\circ&-&\circ&-&\circ&-&\bullet&-&\circ&-&\circ\\
|& & | & & | & & | & & | & & |\\
\circ&-&\circ&-&\circ&-&\bullet&-&\circ&-&\circ\\
|& & | & & | & & | & & | & & |\\
\bullet&-&\circ&-&\bullet&-&\bullet&-&\circ&-&\circ\\
|& & | & & | & & | & & | & & |\\
\circ&-&\circ&-&\circ&-&\bullet&-&\circ&-&\circ\\
|& & | & & | & & | & & | & & |\\
\circ&-&\circ&-&\circ&-&\bullet&-&\circ&-&\bullet\\
|& & | & & | & & | & & | & & |\\
\circ&-&\circ&-&\circ&-&\bullet&-&\circ&-&\circ
\end{matrix}
\end{align}
You can probably guess by now that an exact solution will only come through enumeration for finite sizes. Moreover, as loops are now possible, even statistical treatment becomes hazardous.
Let me make an example, and let's try to compute the distribution $n(s;P)$ in 2-D.
Let's say we can compute $g(s,t)$, the number of clusters of sizes $s$ with perimeter $t$. (The perimeter is the number of adjacent unoccupied sites, in the four directions: e.g. the leftmost cluster in the above figure has $t=3$ neighbours.) Then the distribution will be given by
$$n(s;P)=\sum_{t=1}^\infty g(s,t)(1-P)^t P^s$$
So far so good. The problem is, there is no known way of computing $g(s,t)$ methodically. Moreover, enumeration is tedious, and last time I checked, it had been tabulated up to $s\sim 50$, which is somewhat less than infinity ;).
This is where your question comes in play. If the answer to your problem was known for general sizes, then this very important problem would have a solution as well. But it is not the case (so far, maybe MSE can solve it?!).
Further reading
