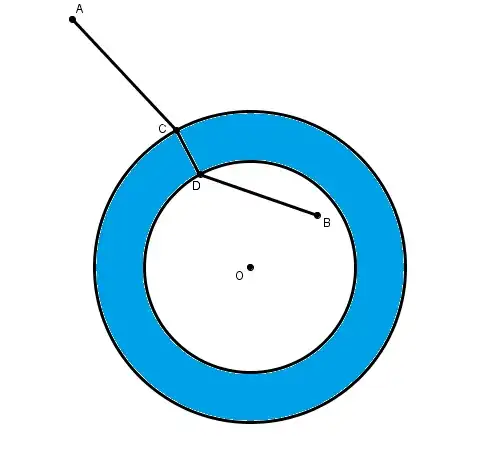
There is a river in the shape of an annulus. Outside the annulus there is town "A" and inside there is town "B". One must build a bridge towards the center of the annulus such that the path from A to B crossing the bridge is the shortest possible. Where to build the bridge?
To take advantage of Snell's law, applying a limit argument: We want to find the trajectory of a light ray where the velocity on the inner and outer terrain is constant (say $v$) and the velocity on the water ($V$) tends to zero.
Assume first that $0< V \ll v$. Then, calling $R_1$, $R_2$ the inner and outer radius, and $A,B,C,D$ the incidence angles (see figure) we have:
$$\frac{\sin A}{\sin B}=\frac{v}{V}=\frac{\sin D}{\sin C}$$
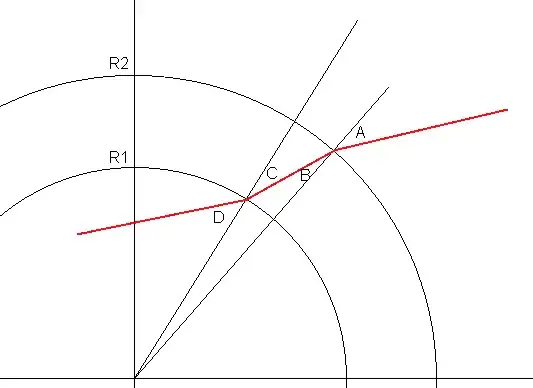
Now, in the limit $V \to 0$ (which is our scenario) we have $$\frac{\tan B}{\tan C} \to \frac{R_1}{R_2} $$ so, because $\tan B/\tan C \to \sin B/\sin C$, the trajectories must follow the relation:
$$ R_2 \sin A = R_1 \sin D $$
What follows is a bit of trygonometry - straightforward to write, but not to find a closed form equation. I doubt that is feasible, I'd go for a iterative numeric solution, though perhaps this is not much better than simply finding the minimum length numerically. I wonder if there is some geometric construction [*].
Update: I didn't notice that this result is already pointed out in a comment by WimC.
[*] Update 2: A nice geometric interpretation (not exactly a construction) is shown in the figure below. Consider the inner segment from the inner incidence point ($d$) to the target point ($Q$), and extend it until it crosses the outer circle (point $I$). Then, consider the triangle $IdO$ (light blue in the figure), and apply to it the law of sines: $\sin A/R_1 = \sin D/R_2$. For the path to be the optimum one, both angles in the figure ($\alpha$ and $\beta$) must be equal. Click here
BTW: A comment in the question conjectures that "one must join $A$ and $B$ (here $P$ and $Q$) and build the bridge where the segment crosses the external circle". That this is false can be seen easily, (independently of this derivation). Suppose that $L$ is the optimum path (red path) joining $P$ and $Q$, then consider an alternative inner point $Q'$ that lies in $L$, "before" $Q$; then the optimum path must cross the river at the same place. This won't happen if one uses the conjectured construction.
(Edited to make coordinates symmetrical about the $x$-axis from the beginning. Also, notation is changed slightly to help distinguish the path's fixed endpoints from the bridge's variable endpoints.)
Take our path to have fixed endpoints $A(a\cos\phi, a\sin\phi)$, $B(b \cos\phi,-b\sin\phi)$ and our bridge to have to-be-determined endpoints $R(r \cos\theta, r\sin\theta)$, $S(s\cos\theta, s\sin\theta)$ (with $a \geq r\geq s \geq b$). Our goal being to find $\theta$ that minimizes $$|AR|+|RS|+|SB|$$ As $|RS| = r-s$ is constant, we "only" need to minimize $$ p:=|AR|+|SB| =\sqrt{a^2+r^2-2a r \cos\left(\theta-\phi\right)}+\sqrt{b^2+s^2-2bs\cos\left(\theta+\phi\right)}$$ The standard calculus approach is to solve for $\theta$ in the equation $$\frac{dp}{d\theta}=0 \qquad\qquad (1)$$ This is considerably easier said than done, as $(1)$ becomes $$ \frac{a r \sin\left(\theta-\phi\right)}{\sqrt{a^2+r^2-2a r\cos\left(\theta-\phi\right)}} = \frac{bs\sin\left(\theta+\phi\right)}{\sqrt{b^2+s^2-2bs \cos\left(\theta+\phi\right)}} \qquad (2)$$ Squaring and "simplifying" gives a long polynomial in $\sin\theta$ AND $\cos\theta$. Another round of squaring and "simplifying" gets us to a polynomial in $\sin\theta$ OR $\cos\theta$, but it's somewhat less-complicated to express the polynomial equation in terms of complex exponentials: $$\sigma := e^{i\phi} = \cos\phi + i \sin\phi \qquad\qquad \tau := e^{i\theta} = \cos\theta + i \sin\theta$$
And here it is after division by $a^2 r^2 b^2 s^2 \sigma^3$ to highlight some symbolic (and "harmonic") symmetry: $$\begin{align} 0 &= \tau^6 \left( \frac{\sigma}{ar} - \frac{\overline{\sigma}}{bs} \right) + \left( \frac{\overline{\sigma}}{ar} - \frac{\sigma}{bs} \right) \\ &- \tau^5 \left( \frac{\sigma^2}{a^2} + \frac{\sigma^2}{r^2} - \frac{\overline{\sigma}^2}{b^2} -\frac{\overline{\sigma}^2}{s^2} \right) - \tau \left( \frac{\overline{\sigma}^2}{a^2} + \frac{\overline{\sigma}^2}{r^2} - \frac{\sigma^2}{b^2} - \frac{\sigma^2}{s^2} \right) \\ &- \tau^4 \left( \frac{2 \overline{\sigma}-\sigma^3}{ar} - \frac{ 2 \sigma - \overline{\sigma}^3 }{bs} \right) - \tau^2 \left( \frac{2 \sigma-\overline{\sigma}^3}{ar} -\frac{2 \overline{\sigma}-\sigma^3}{bs} \right) \\ &+ 2 \tau^3 \left( \frac{1}{a^2}+\frac{1}{r^2} - \frac{1}{b^2} - \frac{1}{s^2} \right) &(\star) \end{align}$$ A sixth-degree polynomial is, in general, symbolically intractable. Maybe there's some trigonometric structure here that gives rise to a symbolic solution, but this is about as far as I go.
Incidentally, in the case where $A$ lies on the outer bank ---that is, when $a=r$--- the polynomial has a double-root $\tau = \sigma$, corresponding to the condition $\theta = \phi$. This matches our expectation that the bridge must extend directly from $A$. (If the bridge were located anywhere else, then the path from $A$ to $R$ would itself pass through the river.)
Likewise, when $B$ lies on the inner bank, we get a double-root $\tau = \overline{\sigma}$; while this corresponds to having the bridge extend from $B$, it's not as obvious that the bridge must do so. (Unlike the $A$-on-the-bank case, a bridge located elsewhere does not require passing through the river to get from $B$ to $S$.)
@leonbloy's answer leverages Snell's Law. As one expects, his relation is equivalent to equation $(2)$ above. Writing $A^\prime$ and $B^\prime$ for the respective feet of perpendiculars from $A$ and $B$ onto $\overleftrightarrow{RS}$, the Snell equation becomes $$r \sin\angle ARA^\prime = s \sin\angle BSB^\prime$$ whereas equation $(2)$ asserts $$\frac{a r \sin\angle AOR}{|AR|} = \frac{b s \sin\angle BOS}{|BS|} $$ Since $$\begin{align} a \sin\angle AOR &= |AA^\prime| = |AR| \sin\angle ARA^\prime \\ b \sin\angle BOS &= |BB^\prime| = |BS| \sin\angle BSB^\prime \end{align}$$ the equations match.
Separating the $ar$ stuff from the $bs$ stuff in the polynomial $(\star)$ gives $$\left(\tau^2\sigma^2 - 1 \right)^2 \left(\frac{\tau}{a} - \frac{\sigma}{r} \right) \left( \frac{\tau}{r} - \frac{\sigma}{a} \right) = \left( \tau^2-\sigma^2 \right)^2 \left( \frac{\tau \sigma}{b} - \frac{1}{s} \right) \left(\frac{\tau\sigma}{s} - \frac{1}{b} \right) \qquad\quad (\star\star)$$ which seems to be trying to tell us something. Unsurprisingly, $(\star\star)$ can ultimately be manipulated into $(2)$, because $(2)$ is the computational essence of the problem. I'm wondering, though, whether $(\star\star)$ encodes geometric insights that help in understanding this result.
I should probably let this go. :)
One more thing ...
Equation $(2)$ can be interpreted geometrically as $$\frac{|\triangle AOR|}{|AR|} = \frac{|\triangle BOS|}{|BS|}$$
which implies that the altitudes of $\triangle AOR$ and $\triangle BOS$ corresponding to edges $AR$ and $BS$ are congruent. This says exactly that $O$ is equidistant from the (extended) edges, so that those (extended) edges must be tangent to some common circle about the origin. This gives us a strategy for finding the bridge.
Build an auxiliary circle (the purple dashed one) and let $Q$ and $R$ be the points where the tangents to that circle from $A$ meet the outer riverbank (blue circle), and let $S$ and $T$ be the points where the tangents from $B$ meet the inner riverbank (red circle). Build bridges at $Q$ and $R$ (in blue), and $S$ and $T$ (in red). Then, simply adjust the size of the auxiliary circle until a blue bridge overlaps a red bridge.
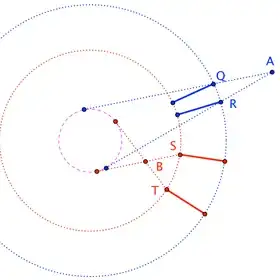$\qquad$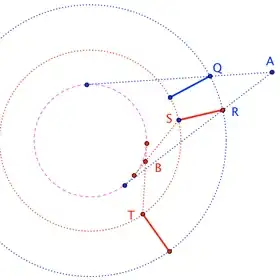 
I think that only two overlaps are ever feasible. (In the diagram, the $T$ bridge never gets close enough to the $Q$ and $R$ bridges ... except in the case of collinear $O$, $A$, $B$ when the auxiliary circle collapses to a point and all bridges coincide.) This seems consistent with a question I posed in a previous edit about whether four of the roots of $(\star)$ are always extraneous.
The problem is equivalent to the famous Alhazen's problem in optics, which was solved geometrically by, among others, Christiaan Huygens:
http://www2.kenyon.edu/Depts/Math/Aydin/Teach/128/AlHazen.pdf
