2

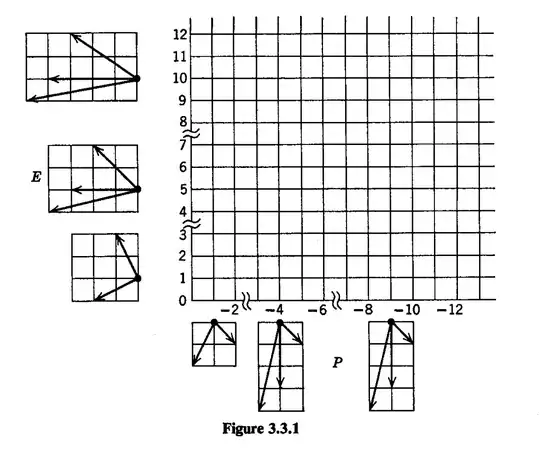
I am working through chapter 3 of Rufus Isaacs's work on differential games which is devoted to discrete games. I am stuck trying to understand his section 3.3 Battles of Extinction game where there are 2 players E and P (E tries to maximize, P to minimize the payoff). I can not understand the moves allowed in the game as shown in the figure 3.3.1 below (in his language If y pertains to the maximizing player E, then the H will be —x on the y-half axis and y on the x-half axis but I cant make sense of this wording)

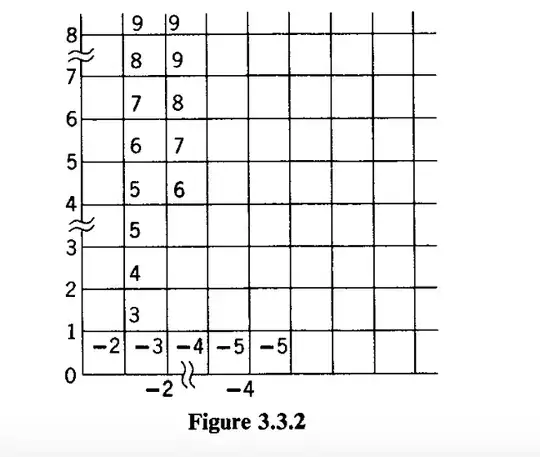
enter image description here

and the payoffs derived and shown in the next figure 3.3.2. enter image description here

What are the rules and goals of the game?

Isaacs, Rufus, Differential games. A mathematical theory with applications to warfare and pursuit, control and optimization., Mineola, NY: Dover Publications (ISBN 0-486-40682-2/pbk). xxii, 384 p. (1999). ZBL1233.91001.

user35202
  • 479

1 Answers1

1

The moves are prescribed/given in figure 3.3.1. The goal is to hit the y=0 or x=0 axes the quickest. So if it is E's turn at the point (y=1,x=-1) and E tries the top allowed move E will end up at (y=3,x=0). If E tries the other allowed move E will end up at (y=0, x=1). E's payoff is then the max of 3 and 1 which is 3.

On the other end if it is P turn at the point (y=1,x=-1) and P does the 2 down 1 left move, P ends at (y=-1,x=0). If it tries the other move 1 right and 1 down, P ends at (y=0,x=-2). P's payoff is then the min of -1 and -2 so it is -2.

If the starting point is (y=1,x=-2) then E can not reach either of the axes. P can however reach the y=0 axis at x=-3 using one of the moves (the other move ends at y=-1,x=-1) so P's payoff is -3.

Proceeding this way we get figure 3.3.2 although there is a typo: P's payoff at (y=1,x=-5) is -6 not -5.

We can also fill other values (not in figure 3.3.2) by using the values in 3.3.2: For example if the starting point is (y=5,x=-1) then P moves lead it to either (y=3,x=0) or (y=4,x=-2). The payoff for E at those points is 3 and 6. So P's payoff is the min of 3 and 6 or 3.

Proceeding this way we can find the payoffs in the entire grid (figure 3.3.3 in the book)

user2175783
  • 310