2

We know that $\mathbb{R^2}$ is a field if we define a multiplication like this: $$(a,b)(c,d)=(ac-bd,ad+bc).$$ But is this multiplication the only multiplication that makes $\mathbb{R^2}$ be a field?

Suppose there is a multiplication makes $\mathbb{R^2}$ be a field, $$e_1=(1,0),e_2=(0,1)$$ and $$x=ae_1+be_2,y=ce_1+de_2,$$ then $$xy=ace_1^2+(ad+bc)e_1e_2+bde_2^2.$$ So this multiplication is uniquely determined by $e_1^2,e_1e_2,e_2^2.$

Can we prove $e_2^2=-1$?

jpmacmanus
  • 833
user1438092
  • 49
  • 5
    This is too vague. What properties of $\mathbb R^2$ do you want the field structure to respect? If you just mean $\mathbb R^2$ as a set, then fix any bijection with $\mathbb R$ that you like and pull back the usual field structure on the real line. – lulu Feb 25 '25 at 12:45
  • I mean $\mathbb{R^2}$ as a vector space. I want to know if there are other multiplications that make $\mathbb{R^2}$ a field. – user1438092 Feb 25 '25 at 12:59
  • Did you mean $e_2^2=-e_1$? Anyway, the answer is NO! Any linear isomorphism $\Bbb{R}^2\to\Bbb{R}^2$ will turn it into a field with a slightly different looking (but still isomorphic) multiplication. – Jyrki Lahtonen Feb 25 '25 at 12:59
  • For a simple example, you can have $e_1^2=e_1$, $e_1e_2=e_2=e_2e_1$, $e_2^2=-4e_1$, when $ae_1+be_2$ corresponds to $a+2bi$. – Jyrki Lahtonen Feb 25 '25 at 13:01
  • See here or even Wikipedia. When the bijection you use to transport the structure is a linear transformation, it will preserve addition as well as multiplication by reals. – Jyrki Lahtonen Feb 25 '25 at 13:10
  • Setting $i^2 = 1$ gives split-complex numbers (used in hyperbolic geometry), and setting $i^2 = 0$ gives dual numbers (used in implicit differentiation). Unfortunately both have zero-divisors so are rings but not fields. – user3257842 Feb 25 '25 at 13:16

2 Answers2

4

What you wrote defines all possible real commutative, (non)-associative algebras of dimension $2$, as I understand it. They are just defined by the multiplication between the basis vectors $e_1$ and $e_2$, as you said, where the product is extended bilinearly. Among them are the complex numbers, and several other algebras, either isomorphic to it, or not a field. This is known from the classification.

References can be found here:

Classification of two dimensional algebras without unit.

A general classification in dimension $2$ can be found here.

Dietrich Burde
  • 140,055
1

A field must have a unit element. Without loss of generality we can assume that element to be: $e_1 = (1, 0)$.
From this we get $e_1^2 = 1$, $e_1e_2 = e_2$.

The only remaining unknown is ${e_2}^2$.
We will denote $e_1 = 1$ and $e_2=i$ for convenience.
Let $i^2 = x + iy$ for some $x$ and $y$.
Our multiplication is:

$$(a+ib)(c+id) = ac +i(ad+bc)+i^2(bd)=\\ =(ac + x\;bd) +i(ad + bc + y\; bd) $$

We will examine how our choice of $x,y$ for $i^2 = x + i\; y$ affects the structure of our algebra. We have: $$(a+ib)^2 = (a^2 + b^2 x) + i(2 a b + b^2 y)$$ Solving $(a+ib)^2 = -1$ gives us:

$$a+ib =\pm \frac{y-i2}{\sqrt{-(4x+y^2)}}$$ Therefore, when (and only when) $i^2 = x+iy$ satisfies $4x+y^2 < 0$, we can set: $a+ib = \frac{y-i2}{\sqrt{-(4x+y^2)}}$ as our new imaginary unit (squaring to -1), and our algebra is isomorphic to the complex numbers. This still leaves $2$ more cases to be examined:

When $i^2 = x+iy$ satisfies $4x+y^2 > 0$, we can solve $(a+ib)^2 = 1$ giving us:

$$a+bi=\pm 1 \;\;\text{or}$$ $$a+ib =\pm \frac{y-i2}{\sqrt{4x+y^2}}$$

Setting $a+ib =\frac{y-i2}{\sqrt{4x+y^2}}$ as our imaginary unit shows this algebra isomorphic to the split-complex numbers .

When $i^2 = x+iy$ satisfies $4x+y^2 = 0$, we can solve $(a+ib)^2 = 0$ giving us: $$a+ib = (\frac{y}{2}-i)*c$$ for any choice of constant factor $c$. Setting $a+ib = y-i 2$ as our new imaginary unit shows the algebra to be isomorphic to the dual numbers.

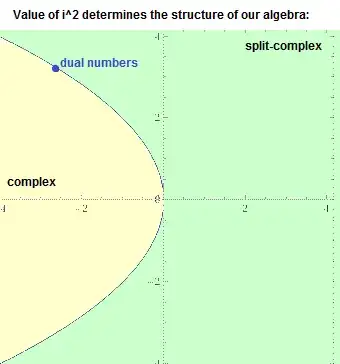
                  enter image description here

In summary, if we set $i^2 = x+iy$, the sign of $4x+y^2$ determines the structure of our algebra:

$4x+y^2 < 0$ makes it isomorphic to the complex numbers, which have $i^2=-1$
$4x+y^2 > 0$ makes it isomorphic to the split-complex numbers, which have $i^2 = 1$
$4x+y^2 = 0$ makes it isomorphic to the dual numbers, which have $i^2 = 0$

A field, in addition to having a unit element must have no divisors of zero.
The split-complex and dual numbers do not satisfy these conditions (eg. $(1+i)(1-i)=0$ for split-complex and $i^2 = 0$ for duals), therefore are not fields.
Therefore, every field structure of $\mathbb{R}^2$ is isomorphic to $\mathbb{C}$.

Dropping the field requirements (existence of a unit element and a lack of zero-divisors) allows for far richer algebraic structures, which have been referenced in the other answer to this question.

user3257842
  • 4,526