Finding a general formula for $n$th term of the sequence such that $a_1 = 2$, $a_2 = 3$, $a_{2k+2} = 2 + a_k + a_{k+1}$, and $a_{2k+1} = 2 + 2a_k$

Question

Problem 1 from the the 39th INMO, 2025.

Consider the sequence defined by $a_1 = 2$, $a_2 = 3$, and $a_{2k+2} = 2 + a_k + a_{k+1}$ and $a_{2k+1} = 2 + 2a_k$ for all integers $k \geq 1$.

Determine all positive integers $n$ such that $a_n/n$ is an integer.

The official solution is available online. I was wondering if it is possible to create a formula for the nth term of this sequence using the information provided, and if there was a solution that did not use the parities of the terms or any modular arithmetic.

My work:

Given that $a_{2k+1} = 2 + 2a_k$

⟹ $a_k = a_{2k+1}/2 - 1$

$k→k+1$

⟹ $a_{k+1} = a_{2k+3}/2 - 1$

Given that $a_{2k+2} = 2 + a_k + a_{k+1}$

Substituting the previous result for $a_k$ and $a_{k+1}$

⟹ $a_{2k+2} = 2 + a_{2k+1}/2 - 1 + a_{2k+3}/2 - 1$

⟹ $2a_{2k+2} = a_{2k+1} + a_{2k+3}$

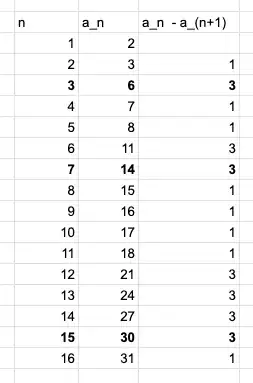
However, since $a_{2k+1}, a_{2k+2}, a_{2k+3}$ are consecutive terms, the relation $2a_{2k+2} = a_{2k+1} + a_{2k+3}$ implies that this is an Arithmetic Progression. Is this true?

Here is a link to the question paper (PDF link via hbcse.tifr.res.in).

Answer 1

$2a_{2k+2} = a_{2k+1} + a_{2k+3}$ implies that this is an Arithmetic Progression.

If you listed out the first few terms (see screenshot below), you might realize that we do not have an arithmetic progression. EG $a_1 = 2, a_2 = 3, a_3 = 2 + 2a_1 = 6$.

To clarify this statement, that equation implies that $a_{2k+1}, a_{2k+2}, a_{2k+3}$ is a 3-term arithmetic progression (for $k \geq 1$). EG We do not have that $a_1, a_2, a_3$ is an AP, which it is not.

Furthermore, just having that equation hold for all $k$ doesn't imply that $a_k$ is an arithmetic progression. In order for us to draw that conclusion, we also need $2a_{2k+1} = a_{2k} + a_{2k+2}$, which we can show is not always true. EG $a_3 = 2 + 2a_1 = 6, a_4 = 2 + a_1 + a_2 = 7$, but $ 2a_3 \neq a_2 + a_4 = 10$.

I was wondering if it is possible to create a formula for the nth term of this sequence using the information provided

If you calculated the first few terms of the sequence and found the first difference (see screenshot below), you might notice a pattern of 1's and 3's. This could lead to the conjecture that for $ n > 3$, let $ 2^m \leq n \leq 2^{m+1} -1$, then we have the formula
$$f(n) = \begin{cases} 2(2^m-1) + (n - 2^m+1) & n < 3 \times 2^m \\ 2(2^{m+1}-1) - 3 (2^{m+1} - 1 - n) & n \geq 3 \times 2^m \end{cases}.$$
This can be proven by (strong) induction.

Corollary: For the original problem, conclude that $\frac{a_n}{n} $ is an integer iff $ n = 2^m - 1$.

Answer 2

I was wondering if it is possible to create a formula for the nth term of this sequence using the information provided, and if there was a solution that did not use the parities of the terms or any modular arithmetic.

Yes and no.

You can concoct a formula which depends only on $n$, but it's a mess. You can print some terms of the sequence, analyse them, and realize that the formula must get information from the number $n$ expressed in a binary form. In the end, you play in a clever way with logarithms, absolute values, floor values, exponentials, etc... in order to extract informations from the binary value and build the function you have to build.

What you get is:

$$a_n = 2(n-1) + 2^{ \lfloor \log_2 n \rfloor} \left(\left| \frac{n}{2^{ \lfloor \log_2 n \rfloor}} - \left\lfloor \frac{n}{2^{ \lfloor \log_2 n \rfloor}} \right \rfloor -\frac{1}{2} \right| -\frac{1}{2} \right)$$

As you see, it is not recursive and uses only $n$, but it is what it is.