Are tetromino packings always 4-colorable?

Question

Suppose that I have a $2n \times 2n$ grid which has had $n^2$ tetrominoes packed into it, as in the following illustration:

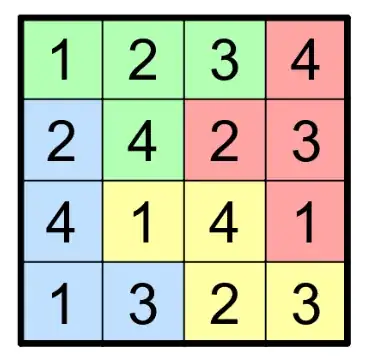
Can I always assign the numbers 1,2,3,4 to the squares of the grid so that (1) each tetromino contains each number exactly once, and (2) orthogonally adjacent squares always receive different numbers? For example, here's a valid coloring of the above packing:

Remarks:

• This can be viewed graph-theoretically as asking for a 4-coloring of the graph $G$ obtained from the $2n \times 2n$ grid graph by "pasting in" copies of $K_4$ on the vertex sets of the tetrominoes. If we were able to paste arbitrary $K_4$s into this graph, then the answer would clearly be "no", since pasting in a $K_4$ on the neighbors of an interior vertex would yield a copy of $K_5$. So any proof of the affirmative would have to specifically use the structure of the tetrominoes.
  • The underlying graph is 4-degenerate (since the grid is 2-degenerate and each tetromino only adds degree at most 2 to each vertex), so you can definitely do it with 5 colors.
  • It's tempting to try and use something like Alon-Tarsi or the kernel method here: the maximum degree in the graph obtained this way is 6, and for a large grid that's going to be very close to the average degree, so it feels like we have just enough room to make an orientation where the max indegree, or max outdegree, is 3. But it seems hard to do that and also enforce any kind of meaningful structure on the orientation that would allow for a coloring argument.
• If there are no T-tetrominoes used in the packing, then since all remaining tetrominoes use exactly 2 white squares and 2 black squares in the natural checkerboard coloring of the grid, it becomes easy to solve this: assign numbers 1,2 to the white squares and 3,4 to the black squares so that each tetromino has exactly one of each number. Since the underlying checkerboard coloring has no adjacent white squares and no adjacent black squares we easily satisfy the grid-adjacency constraint. But the T-tetrominoes throw a wrench in this strategy.
• Similar questions can also be posed for, say, a packing of an odd grid with a square removed, or a different size of polyomino. But this seems to be an interesting particular case.
• I've tested this computationally and -- barring a programming error -- it looks like a 4-coloring is possible for all tetromino packings in a 4x4 or 6x6 grid, or in a 5x5 grid with the center tile removed. The analogous claim also holds for tromino packings into a 6x6 grid: all such packings can be colored using 3 colors.