Prove $1 < \frac{2^{p+1}}{p+1} < 2^p +1$ without using induction

Question

How do I prove that, for every positive integer $p$, $$1 < \frac{2^{p+1}}{p+1} < 2^p +1$$

without using induction, Calculus, Binomial Theorem or Bernoulli's Inequality. I know this can be easily proven using induction but I'd like to prove this directly from theorems regarding exponents. I know that $2^{p+1}>1$ since $p+1\geq 1$. If I can show that, $$2^{p+1}>p+1$$

then, the first half is proven. But I'm not sure how to get here. I'd appreciate any help.

@geetha290krm I should mention that I would prefer not to use binomial theorem — Mohammad muazzam ali, Jan 19 '25 at 09:16
@XK I was hoping to prove this directly from theorems deduced from order axioms and properties of exponents if possible. — Mohammad muazzam ali, Jan 19 '25 at 09:26
Well, if $p\ge 1$, then $$ \frac{{2^{p + 1} }}{{p + 1}} \le \frac{{2^{p + 1} }}{{1 + 1}} = 2^p < 2^p + 1. $$ — Gary, Jan 19 '25 at 09:57
By AM-GM inequality, $$ \frac{{2^{p + 1} }}{{p + 1}} = \frac{{2^{p + 1} + p}}{{p + 1}} - \frac{p}{{p + 1}} > \sqrt[{p + 1}]{{2^{p + 1} \cdot 1 \cdots 1}} - 1 = 1. $$ — Gary, Jan 19 '25 at 10:05
@Gary If I am not wrong, I think the Am-Gm works by induction or via calculus . — , Jan 19 '25 at 10:07
@brokenspirit: You could say that all statements about integers use induction at some point. — Martin R, Jan 19 '25 at 10:16
What "theorems regarding exponents" would you accept? If you define exponentiation by repeated multiplication, i.e., by recursion, then every proof that makes use of the definition involves induction. If you define exponentiation via $e$, you rely on calculus ... — Hagen von Eitzen, Jan 19 '25 at 12:05
I think that for these questions, "proof without induction" means the following: A proof that reduces the statement to be proved to a statement that is "obvious" to the OP (making it a subjective notion), where the reduction cannot explicitly use the induction principle or the well-ordering of the natural numbers, but is allowed to use algebraic or logical operations that are done "in parallel", such as manipulating sums and products. — Bart Michels, Jan 19 '25 at 15:20

score 6 · Accepted Answer · 2025-01-20T08:18:49.070

${\color{#c00}{\rm\bf{New\;proof\;.}}}$

We want to prove a stronger inequality $2^n \ge n+1,\; \forall n\in\Bbb Z^{+}.$

Consider the following construction, which involves a one-to-one correspondence between the terms :

$$ \begin{align}\underbrace{\begin{array}{cccccc} 2 & 2^2 & 2^3 & 2^4 & \dots & 2^n \\ \downarrow & \downarrow & \downarrow & \downarrow & \dots & \downarrow \\ 2 & 2 & 2 & 2 & \dots & 2 \end{array}}_{n\;\text{terms}}\end{align} $$

We can write the following system of inequalities :

$$ \begin{cases}\begin{align}2&~\ge~ 2\\ 2^2&~\ge~2\\ 2^3&~\ge~2\\ 2^4&~\ge~2\\ &\dots\\ 2^n&~\ge~2\end{align}\end{cases} $$

By summing up all inequalities side by side :

$$\small{\underbrace{2+2^2+\dots+2^n}_{n \;\text{terms}}\ge \underbrace{2+2+\dots+2}_{n\;\text{terms}}}$$

Based on the following general geometric structure

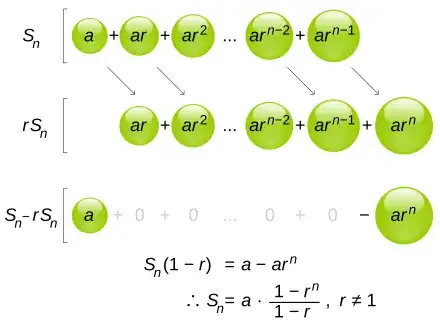
and applying the geometric series formula above, we have :

$$ \begin{align}2^{n+1}-2&\ge 2n\\ 2^{n+1}&\ge 2(n+1)\\ 2^n&\ge n+1\end{align} $$

This completes the proof .

Note that, the right hand side of the inequality has been proven in previous answers and comments .

$\color{#0a0}{\rm\bf{Second\;proof\;.}}$

Note that, $n_0>2^{n_0}$ implies the following inequalities :

$$n_0>2^{n_0}>2^{2^{n_0}}>2^{2^{2^{n_0}}}>\dots$$

which tells us $n_0$ can not be a finite number . A contradiction .

Above, we used the fact that if $m > n$, then $2^m > 2^n$, which follows from the equivalent statement $2^n(2^{m-n} - 1) > 0$ . This is based on the fact that if $k \in \Bbb{Z}^{+}$, then $2^k > 1$ .

$\color{#a0a}{\rm\bf{Old\;proof\;.}}$

Below, we prove the left-hand side of the inequality using the well-known method of Proof by Contradiction . Note that, the same can be applied to the right-hand side as well .

Since the problem statement cannot be false for all $p$, we can assume that there exists a minimum value of $p=p_0\ge1$ for which the statement does not hold .

Let $n_0=\min\{n\}\ge 2$, where $n=p+1$, such that $n_0 \ge 2^{n_0}$ and $n_0\in\Bbb Z$ .

Let

$$n_0-2^{n_0}=k \ge 0$$

By our assumption, we have :

$$ \begin{align}n_0-1-2^{n_0-1}&<0\\ n_0-2^{n_0-1}&<1\\ n_0-\frac{n_0-k}{2}&<1\\ n_0+k&<2\end{align} $$

which is a contradiction .

score 0 · Answer 2 · edited Jan 23 '25 at 17:22

First we can prove directly that $x<2^x$ for $x>1$, from which the left inequality will follow.

Tetration is repeated exponentiation. For example can write something like $^42$ to mean $2^{2^{2^2}}$. We also use the convention $^02=1$. So you can partition numbers greater than $1$ using $[^02,{}^12,{}^22,{}^32,{}^42,\ldots)=[1,2,4,16,65536,\ldots)$.

For any given $x>1$, there is a maximal integer $n$ such that $$^n2\leq x\lt{}^{n+1}2$$

I had to look this up just now, but there is notation for an inverse to tetration, super logarithm. And we can then explicitly define $n=\lfloor\operatorname{slog}_2(x)\rfloor$. This explicit expression for $n$ may avert concerns that this is an induction proof in disguise.

Then raise $2$ to each piece of that triple inequality and since $2^X$ is an increasing function: $${}^{n+1}2\leq2^x\lt{}^{n+2}2$$ These two inequalities both use ${}^{n+1}2$, and we have $x\lt{}^{n+1}2\leq2^x\implies x<2^x$.

In the specific case $x=p+1$, we have $$\begin{align} p+1&\lt 2^{p+1}\\ \implies 1&\lt \frac{2^{p+1}}{p+1} \end{align}$$

Your other inequality is solved well in the comments by @Gary. I will repeat that proof here for the sake of completion.

If $p>1$, then $$\begin{align}\frac{{2^{p + 1}}}{{p + 1}} &\le \frac{{2^{p + 1}}}{{1 + 1}} = 2^p < 2^p + 1\\\implies \frac{{2^{p + 1}}}{{p + 1}}&\lt 2^p+1\end{align}$$

Prove $1 < \frac{2^{p+1}}{p+1} < 2^p +1$ without using induction

2 Answers2