16

Motivated by a random problem on the internet, I got interested in the problem below:

Assume we have a $(2n+1)\times (2n+1)$ square grid. Starting from a square (which could be any of the squares), we just can move either right or left. Of course, note that the first move can be at each of the four directions. What is the length of the longest loop we can have in the grid without revisiting squares?

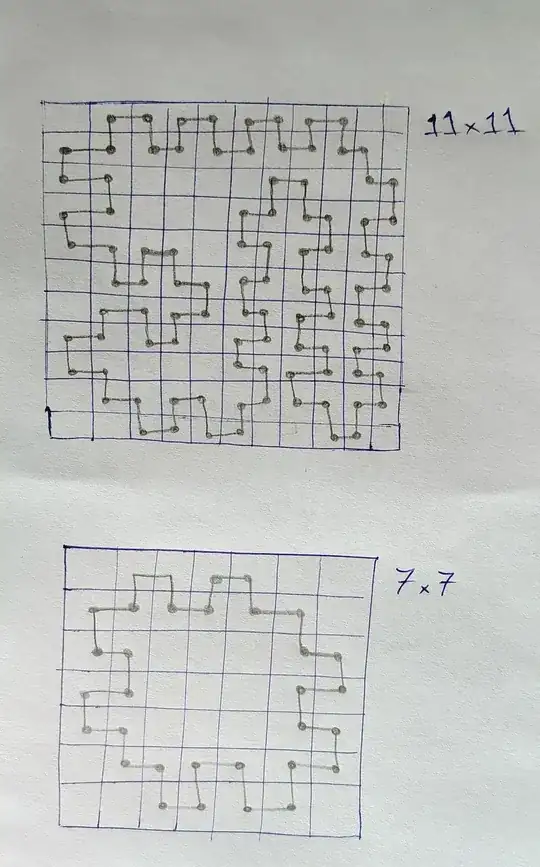
For the sake of clarity, two loops are shown below, which seemingly are the longest possible ones.

After trying a few small $n$'s, it seems that the answer is $(4k)^2$ for $(4k+1) \times (4k+1)$ grids, and $(4k+2)^2-4$ for $(4k+3) \times (4k+3)$ grids. However, I am not certain about my guess because I checked small grids by hand.

enter image description here

There are a few simple facts that can be proved easily. For example, every loop must be a multiple of $4$, or the longest loop can't visit the four corner squares. I tried some sort of induction but it didn't work well while it gives some promising inequalities based on a specific attempt to extend loops. Another idea I was thinking about is Pick's theorem and the enclosed area inside the longest loop.

Considering the statement of the problem, I think this should be a well-studied problem in math competitions or even in recreational mathematics (or even maybe elementary combinatorics); however, I couldn't find anything here.

Any help would be highly appreciated.

Some more thought: Here is another example whose pattern reveals how my guess can be obtained.

enter image description here

Thanks to @RobPratt's comment, I figured out this problem was proposed as a shortlist problem of IMO $2009$. You can see the solution at the IMO official website , Problem C$6$.

RobPratt
  • 50,938
Reza Rajaei
  • 6,236

1 Answers1

7

Like you figured, there are two cases:

  • $n=4k+1$
  • $n=4k+3$

I'll present a representative solution for both cases.

$n=21$

Here's an optimal solution for $n=21$: enter image description here

Note that every 4th square in the path necessarily needs to touch a pink square (because you'll move horizontally/vertically exactly twice). So the longest path touches all $10^2$ pink squares, making the path length $4*10^2$.

$n=23$

enter image description here

Here, there are $11\times11$ pink/red squares. The path must alternate between touching a pink and a red square(??), so one red square square must be missed.

$11^2-1$ pink/red squares are touched, for a total path length of $4(11^2-1)$.

Tom Sirgedas
  • 1,268