Is the probability that the sum of random integers is divisible by $k$ equal to $1/k$?

Question

There are $n$ cards which have numbers $1$~$n$ on each. You pick $m$ cards from it, and you don't put it back once you pick from it. Is the probability that their sum is divisible by $k$ always $\dfrac 1 k$, while $k|n$? If not, how do we generalize the probability?

I've tried to look for the counterexample and found when $n=6, m=3, k=3$. Since the number of cases is $20$, it isn't divisible by 3, so the probability cannot be $\dfrac 1 3$.

Then my question goes,

If not, how do we generalize the probability?

I've tried solving this with a multinomial, but this way, we can't exclude the condition that we don't put it back. (Multinomials should be about independent probabilities, so that's the reason for them, too.)

I tried solving this with Python and found some examples:

Picking 1 card from 1 card - divisible by 1: 1.0
Picking 2 cards from 2 cards - divisible by 1: 1.0
Picking 2 cards from 3 cards - divisible by 1: 1.0
Picking 2 cards from 3 cards - divisible by 3: 0.3333333333333333
Picking 3 cards from 4 cards - divisible by 1: 1.0
Picking 3 cards from 4 cards - divisible by 2: 0.5
Picking 3 cards from 4 cards - divisible by 4: 0.25
Picking 3 cards from 5 cards - divisible by 1: 1.0
Picking 3 cards from 5 cards - divisible by 5: 0.2
Picking 4 cards from 6 cards - divisible by 1: 1.0
Picking 4 cards from 6 cards - divisible by 2: 0.6
Picking 4 cards from 6 cards - divisible by 3: 0.3333333333333333
Picking 4 cards from 6 cards - divisible by 6: 0.2
Picking 4 cards from 7 cards - divisible by 1: 1.0
Picking 4 cards from 7 cards - divisible by 7: 0.14285714285714285
Picking 5 cards from 8 cards - divisible by 1: 1.0
Picking 5 cards from 8 cards - divisible by 2: 0.5
Picking 5 cards from 8 cards - divisible by 4: 0.25
Picking 5 cards from 8 cards - divisible by 8: 0.125
Picking 5 cards from 9 cards - divisible by 1: 1.0
Picking 5 cards from 9 cards - divisible by 3: 0.3333333333333333
Picking 5 cards from 9 cards - divisible by 9: 0.1111111111111111
Picking 6 cards from 10 cards - divisible by 1: 1.0
Picking 6 cards from 10 cards - divisible by 2: 0.47619047619047616
Picking 6 cards from 10 cards - divisible by 5: 0.2
Picking 6 cards from 10 cards - divisible by 10: 0.09523809523809523

Then I found that for prime $p$, $p^n$ has a pattern: $1, 1/p, 1/p^2, \cdots$.

Now I can't find more patterns from this... Any help will be appreciated.

Edit. I decided to try some more, and I got:

Picking 1 card from 1 card - divisible by 1: 1.0
Picking 1 card from 2 cards - divisible by 1: 1.0
Picking 2 cards from 2 cards - divisible by 1: 1.0
Picking 1 card from 2 cards - divisible by 2: 0.5
Picking 2 cards from 2 cards - divisible by 2: 0.0
Picking 1 card from 3 cards - divisible by 1: 1.0
Picking 2 cards from 3 cards - divisible by 1: 1.0
Picking 3 cards from 3 cards - divisible by 1: 1.0
Picking 1 cards from 3 cards - divisible by 2: 0
Picking 2 cards from 3 cards - divisible by 2: 0
Picking 3 cards from 3 cards - divisible by 2: 0
Picking 1 card from 3 cards - divisible by 3: 0.3333333333333333
Picking 2 cards from 3 cards - divisible by 3: 0.3333333333333333
Picking 3 cards from 3 cards - divisible by 3: 1.0
Picking 1 cards from 4 cards - divisible by 1: 1.0
Picking 2 cards from 4 cards - divisible by 1: 1.0
Picking 3 cards from 4 cards - divisible by 1: 1.0
Picking 4 cards from 4 cards - divisible by 1: 1.0
Picking 1 card from 4 cards - divisible by 2: 0.5
Picking 2 cards from 4 cards - divisible by 2: 0.3333333333333333
Picking 3 cards from 4 cards - divisible by 2: 0.5
Picking 4 cards from 4 cards - divisible by 2: 1.0
Picking 1 cards from 4 cards - divisible by 3: 0
Picking 2 cards from 4 cards - divisible by 3: 0
Picking 3 cards from 4 cards - divisible by 3: 0
Picking 4 cards from 4 cards - divisible by 3: 0
Picking 1 card from 4 cards - divisible by 4: 0.25
Picking 2 cards from 4 cards - divisible by 4: 0.16666666666666666
Picking 3 cards from 4 cards - divisible by 4: 0.25
Picking 4 cards from 4 cards - divisible by 4: 0.0
Picking 1 cards from 5 cards - divisible by 1: 1.0
Picking 2 cards from 5 cards - divisible by 1: 1.0
Picking 3 cards from 5 cards - divisible by 1: 1.0
Picking 4 cards from 5 cards - divisible by 1: 1.0
Picking 5 cards from 5 cards - divisible by 1: 1.0
Picking 1 cards from 5 cards - divisible by 2: 0
Picking 2 cards from 5 cards - divisible by 2: 0
Picking 3 cards from 5 cards - divisible by 2: 0
Picking 4 cards from 5 cards - divisible by 2: 0
Picking 5 cards from 5 cards - divisible by 2: 0
Picking 1 cards from 5 cards - divisible by 3: 0
Picking 2 cards from 5 cards - divisible by 3: 0
Picking 3 cards from 5 cards - divisible by 3: 0
Picking 4 cards from 5 cards - divisible by 3: 0
Picking 5 cards from 5 cards - divisible by 3: 0
Picking 1 cards from 5 cards - divisible by 4: 0
Picking 2 cards from 5 cards - divisible by 4: 0
Picking 3 cards from 5 cards - divisible by 4: 0
Picking 4 cards from 5 cards - divisible by 4: 0
Picking 5 cards from 5 cards - divisible by 4: 0
Picking 1 card from 5 cards - divisible by 5: 0.2
Picking 2 cards from 5 cards - divisible by 5: 0.2
Picking 3 cards from 5 cards - divisible by 5: 0.2
Picking 4 cards from 5 cards - divisible by 5: 0.2
Picking 5 cards from 5 cards - divisible by 5: 1.0
Picking 1 cards from 6 cards - divisible by 1: 1.0
Picking 2 cards from 6 cards - divisible by 1: 1.0
Picking 3 cards from 6 cards - divisible by 1: 1.0
Picking 4 cards from 6 cards - divisible by 1: 1.0
Picking 5 cards from 6 cards - divisible by 1: 1.0
Picking 6 cards from 6 cards - divisible by 1: 1.0
Picking 1 card from 6 cards - divisible by 2: 0.5
Picking 2 cards from 6 cards - divisible by 2: 0.4
Picking 3 cards from 6 cards - divisible by 2: 0.5
Picking 4 cards from 6 cards - divisible by 2: 0.6
Picking 5 cards from 6 cards - divisible by 2: 0.5
Picking 6 cards from 6 cards - divisible by 2: 0.0
Picking 1 card from 6 cards - divisible by 3: 0.3333333333333333
Picking 2 cards from 6 cards - divisible by 3: 0.3333333333333333
Picking 3 cards from 6 cards - divisible by 3: 0.4
Picking 4 cards from 6 cards - divisible by 3: 0.3333333333333333
Picking 5 cards from 6 cards - divisible by 3: 0.3333333333333333
Picking 6 cards from 6 cards - divisible by 3: 1.0
Picking 1 cards from 6 cards - divisible by 4: 0
Picking 2 cards from 6 cards - divisible by 4: 0
Picking 3 cards from 6 cards - divisible by 4: 0
Picking 4 cards from 6 cards - divisible by 4: 0
Picking 5 cards from 6 cards - divisible by 4: 0
Picking 6 cards from 6 cards - divisible by 4: 0
Picking 1 cards from 6 cards - divisible by 5: 0
Picking 2 cards from 6 cards - divisible by 5: 0
Picking 3 cards from 6 cards - divisible by 5: 0
Picking 4 cards from 6 cards - divisible by 5: 0
Picking 5 cards from 6 cards - divisible by 5: 0
Picking 6 cards from 6 cards - divisible by 5: 0
Picking 1 cards from 6 cards - divisible by 6: 0.16666666666666666
Picking 2 cards from 6 cards - divisible by 6: 0.13333333333333333
Picking 3 cards from 6 cards - divisible by 6: 0.2
Picking 4 cards from 6 cards - divisible by 6: 0.2
Picking 5 cards from 6 cards - divisible by 6: 0.16666666666666666
Picking 6 cards from 6 cards - divisible by 6: 0.0
Picking 1 cards from 7 cards - divisible by 1: 1.0
Picking 2 cards from 7 cards - divisible by 1: 1.0
Picking 3 cards from 7 cards - divisible by 1: 1.0
Picking 4 cards from 7 cards - divisible by 1: 1.0
Picking 5 cards from 7 cards - divisible by 1: 1.0
Picking 6 cards from 7 cards - divisible by 1: 1.0
Picking 7 cards from 7 cards - divisible by 1: 1.0
Picking 1 cards from 7 cards - divisible by 2: 0
Picking 2 cards from 7 cards - divisible by 2: 0
Picking 3 cards from 7 cards - divisible by 2: 0
Picking 4 cards from 7 cards - divisible by 2: 0
Picking 5 cards from 7 cards - divisible by 2: 0
Picking 6 cards from 7 cards - divisible by 2: 0
Picking 7 cards from 7 cards - divisible by 2: 0
Picking 1 cards from 7 cards - divisible by 3: 0
Picking 2 cards from 7 cards - divisible by 3: 0
Picking 3 cards from 7 cards - divisible by 3: 0
Picking 4 cards from 7 cards - divisible by 3: 0
Picking 5 cards from 7 cards - divisible by 3: 0
Picking 6 cards from 7 cards - divisible by 3: 0
Picking 7 cards from 7 cards - divisible by 3: 0
Picking 1 cards from 7 cards - divisible by 4: 0
Picking 2 cards from 7 cards - divisible by 4: 0
Picking 3 cards from 7 cards - divisible by 4: 0
Picking 4 cards from 7 cards - divisible by 4: 0
Picking 5 cards from 7 cards - divisible by 4: 0
Picking 6 cards from 7 cards - divisible by 4: 0
Picking 7 cards from 7 cards - divisible by 4: 0
Picking 1 cards from 7 cards - divisible by 5: 0
Picking 2 cards from 7 cards - divisible by 5: 0
Picking 3 cards from 7 cards - divisible by 5: 0
Picking 4 cards from 7 cards - divisible by 5: 0
Picking 5 cards from 7 cards - divisible by 5: 0
Picking 6 cards from 7 cards - divisible by 5: 0
Picking 7 cards from 7 cards - divisible by 5: 0
Picking 1 cards from 7 cards - divisible by 6: 0
Picking 2 cards from 7 cards - divisible by 6: 0
Picking 3 cards from 7 cards - divisible by 6: 0
Picking 4 cards from 7 cards - divisible by 6: 0
Picking 5 cards from 7 cards - divisible by 6: 0
Picking 6 cards from 7 cards - divisible by 6: 0
Picking 7 cards from 7 cards - divisible by 6: 0
Picking 1 cards from 7 cards - divisible by 7: 0.14285714285714285
Picking 2 cards from 7 cards - divisible by 7: 0.14285714285714285
Picking 3 cards from 7 cards - divisible by 7: 0.14285714285714285
Picking 4 cards from 7 cards - divisible by 7: 0.14285714285714285
Picking 5 cards from 7 cards - divisible by 7: 0.14285714285714285
Picking 6 cards from 7 cards - divisible by 7: 0.14285714285714285
Picking 7 cards from 7 cards - divisible by 7: 1.0
Picking 1 cards from 8 cards - divisible by 1: 1.0
Picking 2 cards from 8 cards - divisible by 1: 1.0
Picking 3 cards from 8 cards - divisible by 1: 1.0
Picking 4 cards from 8 cards - divisible by 1: 1.0
Picking 5 cards from 8 cards - divisible by 1: 1.0
Picking 6 cards from 8 cards - divisible by 1: 1.0
Picking 7 cards from 8 cards - divisible by 1: 1.0
Picking 8 cards from 8 cards - divisible by 1: 1.0
Picking 1 card from 8 cards - divisible by 2: 0.5
Picking 2 cards from 8 cards - divisible by 2: 0.42857142857142855
Picking 3 cards from 8 cards - divisible by 2: 0.5
Picking 4 cards from 8 cards - divisible by 2: 0.5428571428571428
Picking 5 cards from 8 cards - divisible by 2: 0.5
Picking 6 cards from 8 cards - divisible by 2: 0.42857142857142855
Picking 7 cards from 8 cards - divisible by 2: 0.5
Picking 8 cards from 8 cards - divisible by 2: 1.0
Picking 1 cards from 8 cards - divisible by 3: 0
Picking 2 cards from 8 cards - divisible by 3: 0
Picking 3 cards from 8 cards - divisible by 3: 0
Picking 4 cards from 8 cards - divisible by 3: 0
Picking 5 cards from 8 cards - divisible by 3: 0
Picking 6 cards from 8 cards - divisible by 3: 0
Picking 7 cards from 8 cards - divisible by 3: 0
Picking 8 cards from 8 cards - divisible by 3: 0
Picking 1 card from 8 cards - divisible by 4: 0.25
Picking 2 cards from 8 cards - divisible by 4: 0.21428571428571427
Picking 3 cards from 8 cards - divisible by 4: 0.25
Picking 4 cards from 8 cards - divisible by 4: 0.2571428571428571
Picking 5 cards from 8 cards - divisible by 4: 0.25
Picking 6 cards from 8 cards - divisible by 4: 0.21428571428571427
Picking 7 cards from 8 cards - divisible by 4: 0.25
Picking 8 cards from 8 cards - divisible by 4: 1.0
Picking 1 cards from 8 cards - divisible by 5: 0
Picking 2 cards from 8 cards - divisible by 5: 0
Picking 3 cards from 8 cards - divisible by 5: 0
Picking 4 cards from 8 cards - divisible by 5: 0
Picking 5 cards from 8 cards - divisible by 5: 0
Picking 6 cards from 8 cards - divisible by 5: 0
Picking 7 cards from 8 cards - divisible by 5: 0
Picking 8 cards from 8 cards - divisible by 5: 0
Picking 1 cards from 8 cards - divisible by 6: 0
Picking 2 cards from 8 cards - divisible by 6: 0
Picking 3 cards from 8 cards - divisible by 6: 0
Picking 4 cards from 8 cards - divisible by 6: 0
Picking 5 cards from 8 cards - divisible by 6: 0
Picking 6 cards from 8 cards - divisible by 6: 0
Picking 7 cards from 8 cards - divisible by 6: 0
Picking 8 cards from 8 cards - divisible by 6: 0
Picking 1 cards from 8 cards - divisible by 7: 0
Picking 2 cards from 8 cards - divisible by 7: 0
Picking 3 cards from 8 cards - divisible by 7: 0
Picking 4 cards from 8 cards - divisible by 7: 0
Picking 5 cards from 8 cards - divisible by 7: 0
Picking 6 cards from 8 cards - divisible by 7: 0
Picking 7 cards from 8 cards - divisible by 7: 0
Picking 8 cards from 8 cards - divisible by 7: 0
Picking 1 card from 8 cards - divisible by 8: 0.125
Picking 2 cards from 8 cards - divisible by 8: 0.10714285714285714
Picking 3 cards from 8 cards - divisible by 8: 0.125
Picking 4 cards from 8 cards - divisible by 8: 0.12857142857142856
Picking 5 cards from 8 cards - divisible by 8: 0.125
Picking 6 cards from 8 cards - divisible by 8: 0.10714285714285714
Picking 7 cards from 8 cards - divisible by 8: 0.125
Picking 8 cards from 8 cards - divisible by 8: 0.0
Picking 1 cards from 9 cards - divisible by 1: 1.0
Picking 2 cards from 9 cards - divisible by 1: 1.0
Picking 3 cards from 9 cards - divisible by 1: 1.0
Picking 4 cards from 9 cards - divisible by 1: 1.0
Picking 5 cards from 9 cards - divisible by 1: 1.0
Picking 6 cards from 9 cards - divisible by 1: 1.0
Picking 7 cards from 9 cards - divisible by 1: 1.0
Picking 8 cards from 9 cards - divisible by 1: 1.0
Picking 9 cards from 9 cards - divisible by 1: 1.0
Picking 1 cards from 9 cards - divisible by 2: 0
Picking 2 cards from 9 cards - divisible by 2: 0
Picking 3 cards from 9 cards - divisible by 2: 0
Picking 4 cards from 9 cards - divisible by 2: 0
Picking 5 cards from 9 cards - divisible by 2: 0
Picking 6 cards from 9 cards - divisible by 2: 0
Picking 7 cards from 9 cards - divisible by 2: 0
Picking 8 cards from 9 cards - divisible by 2: 0
Picking 9 cards from 9 cards - divisible by 2: 0
Picking 1 cards from 9 cards - divisible by 3: 0.3333333333333333
Picking 2 cards from 9 cards - divisible by 3: 0.3333333333333333
Picking 3 cards from 9 cards - divisible by 3: 0.35714285714285715
Picking 4 cards from 9 cards - divisible by 3: 0.3333333333333333
Picking 5 cards from 9 cards - divisible by 3: 0.3333333333333333
Picking 6 cards from 9 cards - divisible by 3: 0.35714285714285715
Picking 7 cards from 9 cards - divisible by 3: 0.3333333333333333
Picking 8 cards from 9 cards - divisible by 3: 0.3333333333333333
Picking 9 cards from 9 cards - divisible by 3: 1.0
Picking 1 cards from 9 cards - divisible by 4: 0
Picking 2 cards from 9 cards - divisible by 4: 0
Picking 3 cards from 9 cards - divisible by 4: 0
Picking 4 cards from 9 cards - divisible by 4: 0
Picking 5 cards from 9 cards - divisible by 4: 0
Picking 6 cards from 9 cards - divisible by 4: 0
Picking 7 cards from 9 cards - divisible by 4: 0
Picking 8 cards from 9 cards - divisible by 4: 0
Picking 9 cards from 9 cards - divisible by 4: 0
Picking 1 cards from 9 cards - divisible by 5: 0
Picking 2 cards from 9 cards - divisible by 5: 0
Picking 3 cards from 9 cards - divisible by 5: 0
Picking 4 cards from 9 cards - divisible by 5: 0
Picking 5 cards from 9 cards - divisible by 5: 0
Picking 6 cards from 9 cards - divisible by 5: 0
Picking 7 cards from 9 cards - divisible by 5: 0
Picking 8 cards from 9 cards - divisible by 5: 0
Picking 9 cards from 9 cards - divisible by 5: 0
Picking 1 cards from 9 cards - divisible by 6: 0
Picking 2 cards from 9 cards - divisible by 6: 0
Picking 3 cards from 9 cards - divisible by 6: 0
Picking 4 cards from 9 cards - divisible by 6: 0
Picking 5 cards from 9 cards - divisible by 6: 0
Picking 6 cards from 9 cards - divisible by 6: 0
Picking 7 cards from 9 cards - divisible by 6: 0
Picking 8 cards from 9 cards - divisible by 6: 0
Picking 9 cards from 9 cards - divisible by 6: 0
Picking 1 cards from 9 cards - divisible by 7: 0
Picking 2 cards from 9 cards - divisible by 7: 0
Picking 3 cards from 9 cards - divisible by 7: 0
Picking 4 cards from 9 cards - divisible by 7: 0
Picking 5 cards from 9 cards - divisible by 7: 0
Picking 6 cards from 9 cards - divisible by 7: 0
Picking 7 cards from 9 cards - divisible by 7: 0
Picking 8 cards from 9 cards - divisible by 7: 0
Picking 9 cards from 9 cards - divisible by 7: 0
Picking 1 cards from 9 cards - divisible by 8: 0
Picking 2 cards from 9 cards - divisible by 8: 0
Picking 3 cards from 9 cards - divisible by 8: 0
Picking 4 cards from 9 cards - divisible by 8: 0
Picking 5 cards from 9 cards - divisible by 8: 0
Picking 6 cards from 9 cards - divisible by 8: 0
Picking 7 cards from 9 cards - divisible by 8: 0
Picking 8 cards from 9 cards - divisible by 8: 0
Picking 9 cards from 9 cards - divisible by 8: 0
Picking 1 cards from 9 cards - divisible by 9: 0.1111111111111111
Picking 2 cards from 9 cards - divisible by 9: 0.1111111111111111
Picking 3 cards from 9 cards - divisible by 9: 0.11904761904761904
Picking 4 cards from 9 cards - divisible by 9: 0.1111111111111111
Picking 5 cards from 9 cards - divisible by 9: 0.1111111111111111
Picking 6 cards from 9 cards - divisible by 9: 0.11904761904761904
Picking 7 cards from 9 cards - divisible by 9: 0.1111111111111111
Picking 8 cards from 9 cards - divisible by 9: 0.1111111111111111
Picking 9 cards from 9 cards - divisible by 9: 1.0
Picking 1 cards from 10 cards - divisible by 1: 1.0
Picking 2 cards from 10 cards - divisible by 1: 1.0
Picking 3 cards from 10 cards - divisible by 1: 1.0
Picking 4 cards from 10 cards - divisible by 1: 1.0
Picking 5 cards from 10 cards - divisible by 1: 1.0
Picking 6 cards from 10 cards - divisible by 1: 1.0
Picking 7 cards from 10 cards - divisible by 1: 1.0
Picking 8 cards from 10 cards - divisible by 1: 1.0
Picking 9 cards from 10 cards - divisible by 1: 1.0
Picking 10 cards from 10 cards - divisible by 1: 1.0
Picking 1 card from 10 cards - divisible by 2: 0.5
Picking 2 cards from 10 cards - divisible by 2: 0.4444444444444444
Picking 3 cards from 10 cards - divisible by 2: 0.5
Picking 4 cards from 10 cards - divisible by 2: 0.5238095238095238
Picking 5 cards from 10 cards - divisible by 2: 0.5
Picking 6 cards from 10 cards - divisible by 2: 0.47619047619047616
Picking 7 cards from 10 cards - divisible by 2: 0.5
Picking 8 cards from 10 cards - divisible by 2: 0.5555555555555556
Picking 9 cards from 10 cards - divisible by 2: 0.5
Picking 10 cards from 10 cards - divisible by 2: 0.0
Picking 1 cards from 10 cards - divisible by 3: 0
Picking 2 cards from 10 cards - divisible by 3: 0
Picking 3 cards from 10 cards - divisible by 3: 0
Picking 4 cards from 10 cards - divisible by 3: 0
Picking 5 cards from 10 cards - divisible by 3: 0
Picking 6 cards from 10 cards - divisible by 3: 0
Picking 7 cards from 10 cards - divisible by 3: 0
Picking 8 cards from 10 cards - divisible by 3: 0
Picking 9 cards from 10 cards - divisible by 3: 0
Picking 10 cards from 10 cards - divisible by 3: 0
Picking 1 cards from 10 cards - divisible by 4: 0
Picking 2 cards from 10 cards - divisible by 4: 0
Picking 3 cards from 10 cards - divisible by 4: 0
Picking 4 cards from 10 cards - divisible by 4: 0
Picking 5 cards from 10 cards - divisible by 4: 0
Picking 6 cards from 10 cards - divisible by 4: 0
Picking 7 cards from 10 cards - divisible by 4: 0
Picking 8 cards from 10 cards - divisible by 4: 0
Picking 9 cards from 10 cards - divisible by 4: 0
Picking 10 cards from 10 cards - divisible by 4: 0
Picking 1 card from 10 cards - divisible by 5: 0.2
Picking 2 cards from 10 cards - divisible by 5: 0.2
Picking 3 cards from 10 cards - divisible by 5: 0.2
Picking 4 cards from 10 cards - divisible by 5: 0.2
Picking 5 cards from 10 cards - divisible by 5: 0.20634920634920634
Picking 6 cards from 10 cards - divisible by 5: 0.2
Picking 7 cards from 10 cards - divisible by 5: 0.2
Picking 8 cards from 10 cards - divisible by 5: 0.2
Picking 9 cards from 10 cards - divisible by 5: 0.2
Picking 10 cards from 10 cards - divisible by 5: 1.0
Picking 1 cards from 10 cards - divisible by 6: 0
Picking 2 cards from 10 cards - divisible by 6: 0
Picking 3 cards from 10 cards - divisible by 6: 0
Picking 4 cards from 10 cards - divisible by 6: 0
Picking 5 cards from 10 cards - divisible by 6: 0
Picking 6 cards from 10 cards - divisible by 6: 0
Picking 7 cards from 10 cards - divisible by 6: 0
Picking 8 cards from 10 cards - divisible by 6: 0
Picking 9 cards from 10 cards - divisible by 6: 0
Picking 10 cards from 10 cards - divisible by 6: 0
Picking 1 cards from 10 cards - divisible by 7: 0
Picking 2 cards from 10 cards - divisible by 7: 0
Picking 3 cards from 10 cards - divisible by 7: 0
Picking 4 cards from 10 cards - divisible by 7: 0
Picking 5 cards from 10 cards - divisible by 7: 0
Picking 6 cards from 10 cards - divisible by 7: 0
Picking 7 cards from 10 cards - divisible by 7: 0
Picking 8 cards from 10 cards - divisible by 7: 0
Picking 9 cards from 10 cards - divisible by 7: 0
Picking 10 cards from 10 cards - divisible by 7: 0
Picking 1 cards from 10 cards - divisible by 8: 0
Picking 2 cards from 10 cards - divisible by 8: 0
Picking 3 cards from 10 cards - divisible by 8: 0
Picking 4 cards from 10 cards - divisible by 8: 0
Picking 5 cards from 10 cards - divisible by 8: 0
Picking 6 cards from 10 cards - divisible by 8: 0
Picking 7 cards from 10 cards - divisible by 8: 0
Picking 8 cards from 10 cards - divisible by 8: 0
Picking 9 cards from 10 cards - divisible by 8: 0
Picking 10 cards from 10 cards - divisible by 8: 0
Picking 1 cards from 10 cards - divisible by 9: 0
Picking 2 cards from 10 cards - divisible by 9: 0
Picking 3 cards from 10 cards - divisible by 9: 0
Picking 4 cards from 10 cards - divisible by 9: 0
Picking 5 cards from 10 cards - divisible by 9: 0
Picking 6 cards from 10 cards - divisible by 9: 0
Picking 7 cards from 10 cards - divisible by 9: 0
Picking 8 cards from 10 cards - divisible by 9: 0
Picking 9 cards from 10 cards - divisible by 9: 0
Picking 10 cards from 10 cards - divisible by 9: 0
Picking 1 card from 10 cards - divisible by 10: 0.1
Picking 2 cards from 10 cards - divisible by 10: 0.08888888888888889
Picking 3 cards from 10 cards - divisible by 10: 0.1
Picking 4 cards from 10 cards - divisible by 10: 0.10476190476190476
Picking 5 cards from 10 cards - divisible by 10: 0.10317460317460317
Picking 6 cards from 10 cards - divisible by 10: 0.09523809523809523
Picking 7 cards from 10 cards - divisible by 10: 0.1
Picking 8 cards from 10 cards - divisible by 10: 0.1111111111111111
Picking 9 cards from 10 cards - divisible by 10: 0.1
Picking 10 cards from 10 cards - divisible by 10: 0.0

Well, now I see that(as in the answer below) most of them are the value of $\dfrac 1 k$. Now again my question focuses on:

When do the exceptions occur? For the exceptions, how to treat them?

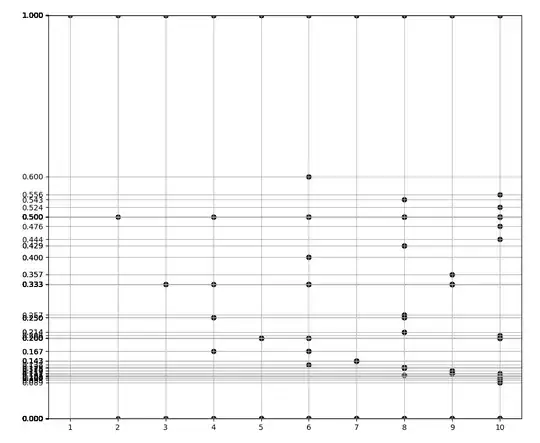
Edit 2. I plotted a graph, with $n$ in the $x$-axis and the probability in the $y$-axis.

What can we get from this? I did this because it seems to need a visualization to solve this.

Answer 1

Not an immediate answer, but an interesting observation: if $\operatorname{gcd}(m,n)=1$ then the probability is equal to $\frac{1}{k}$.

This can be seen as follows. Suppose we have any subset $S=\{s_1,s_2, \ldots, s_m\}$. Consider the subsets $S_i=\{(s_1+i)\mod n, (s_2+i)\mod n, \ldots, (s_m+i)\mod n\}$ for $i=1,2,\ldots, n-1,n$. The sums of the elements of $S_i$ are all distinct modulo $n$ for different $i$ because $\operatorname{gcd}(m,n)=1$. It follows that we can divide the subsets of size $m$ into groups of $n$ subsets each, where each modulo occurs once in each group. So we have the same probability of getting a sum of $i\mod n$ for each $i$, and therefore a probability of $\frac{1}{k}$ to be divisible by $k$ if $k|n$.

Answer 2

This was a beautiful problem to solve. Thank you very much. I have a complete solution, but I strongly encourage everyone to try to solve it on their own. If you wish to do so, leave now or read the "key observation" below if you want a hint.

I have written two detailed posts on my blog in which I go into more details:

• A simulation study

• A detailed mathematical analysis with the final result

---

The key observation

The key observation is due to @Matthew Spam.

• Going from a given a subset $(x_1 \dots x_m)$ to the subset $(x_1 + i \dots x_m + i)$ shifts the final result by $m * i \bmod k$. Thus, we can reach all values that are offset from the initial result by $\operatorname{gcd}(m, k)$.

Again, it is really worth to try to solve this problem by yourself. Trying to figure out how to use this fact is really instructive.

---

Answer: a sufficient condition for $p=1/k$

When $\operatorname{gcd}(m, k) = 1$, the probability is $p=1/k$.

Proof: the observation by Matthew is already sufficient to conclude. It shows that the number of subsets summing to any value in $[0, k-1]$ is equal: i.e. the distribution of $\sum X_i \bmod k$ is uniform.

Is the condition necessary

Yes, sort of. When the gcd is not $1$, the probability can be explicitly computed. It's a bit simpler than proposed by @user2661923 because we do not need to look at every single case like they proposed.

I won't deal with the most general case here: please refer to my blog post; I hope it does a good-enough job because this is a complex solution.

Let's focus on the case where $k$ is prime and $\geq 3$.

A simple case

The values can be decomposed into $n/k$ groups. Let $c_i$ be the count of values in the i-th group. We will compute the desired probability conditional on the $c_i$.

1. If any $c_i$ is $1$, then conditionally $p=1/k$.

   1. Proof: repeat the symmetry argument, but this time only shifting the value $x_i$ inside of its group. This shifts the final sum by $1$, giving us the symmetry.
   2. This is not the most generic case.

2. If $\operatorname{gcd}(k, c_1, c_2 \dots) = 1$, then conditionally $p=1/k$. NB: excluding 0 counts.

   1. Proof: repeat the symmetry argument: shift each value inside of its own group. This modifies the sum by adding $c_1 * i_1 + c_2 * i_2 + \dots$. By definition of the gcd, we can reach any value.

3. When does the condition $\operatorname{gcd}(k, c_1, c_2 \dots) = 1$ not occur? When all counts are either $0$ or $k$.

   1. In this situation, there is no randomness left. The sum is simply: $k (k-1) / 2 * n / k$. This is divisible by $k$ thus, conditionally $p=1$.

We can now conclude:

• Conditional on the event $A$: "all counts are exactly $k$", $p=1$.
• Else, $p=1/k$.

Thus, the unconditional probability is such that: $p > 1/k$. The offset depends on the probability of the event $A$ which goes to $0$ as $n$ grows.

$$ p = p(A) + (1-p(A)) \frac{1}{k} = \frac{1}{k} + p(A) \frac{k-1}{k} $$

Answer 3

By my analysis, a closed form formula is feasible. However, the math that I derived is very ugly. It will be interesting to see if someone can come up with a more elegant closed form formula.

For what it's worth, this answer does not require that $~n~$ be a multiple of $~k.$

For ease of syntax, this answer adopts the convention that when $~a < b,~$ that $~\displaystyle \binom{a}{b} = 0.$

Label the cards, so that $~C_i~$ denotes the card with the number $~i~$ on it, where $~i \in \{1,2,\cdots,n\}.~$

Assume that the $~m~$ cards selected are specifically the cards $~C_{x_1}, ~C_{x_2}, ~\cdots, ~C_{x_m},~$ where $~x_1, ~x_2, \cdots, x_m~$ are distinct elements in $~\{1,2,\cdots,n\},~$ which are in strictly ascending order.

Then, a lower bound on $~\displaystyle \sum_{i=1}^m x_i~$ is $~0,~$ and an upper bound on $~\displaystyle \sum_{i=1}^m x_i~$ is

$$n + (n-1) + \cdots + (n+1-m) = nm - \frac{(m-1)m}{2} = \frac{m(2n+1-m)}{2}.$$

Let $~\lfloor u\rfloor~$ refer to the floor function, for $~u \in \Bbb{R}.$

Let $~\displaystyle A = \left\lfloor \frac{m(2n+1-m)}{2k} ~\right\rfloor.$

For $~r \in \{0,1,2,\cdots,A\},~$ let $~f(r)~$ denote the number of solutions to

• $x_1 + x_2 + \cdots + x_m = r \times k.$

• $x_1, ~x_2, ~\cdots, ~x_m \in \{1,2,\cdots,n\}.$

• $x_1, ~x_2, ~\cdots, ~x_m~$ are in strictly ascending order.

Then, the probability that $~m~$ numbers chosen at random (sampling without replacement) from $~\{1,2,\cdots,n\}~$ will have a sum divisible by $~k~$ is

$$\frac{\sum_{r = 0}^A f(r)}{\binom{n}{m}}. \tag1 $$

So, the entire problem reduces to computing $~f(r).~$ The chief difficulty here is that $~x_1, ~x_2, ~\cdots, ~x_m~$ must be distinct (and therefore in ascending order, rather than in non-decreasing order).

---

Personally, my knowledge of Combinatorics tools is very limited. For example, I am ignorant about generating functions. The only way that I know how to solve this is very ugly.

Let:

• $y_1 = x_1.$

• $y_{i+1} = x_{i+1} - x_i ~: ~i \in \{1,2,\cdots,m-1\}.$

Then, for $~i \in \{1,2,\cdots,m\},~$ you have that $~\displaystyle x_i = \sum_{a=1}^i y_a.$

Therefore, the enumeration of $~f(r)~$ has been transformed into enumerating the number of solutions to:

• $~my_1 + (m-1)y_2 + \cdots + 2y_{m-1} + y_m = rk.$

• $~y_1, ~y_2, ~\cdots, y_m \in \Bbb{Z_{\geq 1}}.$

The first thing to do is adjust each of the variables so that their lower bound is $~0,~$ rather than $~1.~$

So, $~f(r)~$ is the enumeration of the number of solutions to:

• $~my_1 + (m-1)y_2 + \cdots + 2y_{m-1} + y_m = rk - \dfrac{m(m+1)}{2}.$

• $~y_1, ~y_2, ~\cdots, y_m \in \Bbb{Z_{\geq 0}}.$

If $~rk - \dfrac{m(m+1)}{2} < 0,~$ then $~f(r) = 0.~$

So, you can assume, without loss of generality, that $~rk - \dfrac{m(m+1)}{2} \geq 0,~$ in which case the lower bound on each of $~y_1, ~y_2, ~\cdots, ~y_m~$ is $~0.$

Given any positive integers $~s,t~$ define $~\displaystyle g(s,t) = \left\lfloor \frac{s}{t} ~\right\rfloor.~$

Then, the upper bound for $~y_1~$ is $~\displaystyle g\left( ~rk - \frac{m(m+1)}{2}, ~m ~\right).$

Assume that $~y_1~$ is any integer in the appropriate range. Then, based on the specific value chosen for $~y_1,~$ the upper bound for $~y_2~$ is $~\displaystyle g\left( ~rk - \frac{m(m+1)}{2} - my_1, ~m-1 ~\right).$

Similarly, for $~p \in \{2,3,\cdots,m-1\},~$ assuming that the variables $~y_1, y_2, \cdots, y_{p-1}~$ are all integers in range, then the upper bound for $~y_p~$ is

$$g\left( rk - \frac{m(m+1)}{2} - \sum_{i=1}^{p-1} (m+1-i)y_i ~, ~~~~~~m+1-p ~\right).$$

Once $~y_1, ~y_2, \cdots, ~y_{m-1}~$ are chosen, then $~y_m~$ is determined.

So,

$$f(r) = \sum_{y_1 ~\text{in range}} ~\left\{ ~\sum_{y_2 ~\text{in range}} ~\left[ ~\sum_{y_3 ~\text{in range}} \cdots ~\left( ~\sum_{y_{(m-1)} ~\text{in range}} ~1 ~\right) ~\cdots ~\right] ~\right\}.$$

---

Obviously, the algorithm requires computer assistance to compute. The corresponding computer program will be somewhat more complicated to program than just a simple $~m$-nested looping of $~x_1, ~\cdots, ~x_m~$ where you check each occurrence of $~\displaystyle \sum_{i=1}^m x_i.~$

However, unless I am mistaken, the corresponding computer program will (in effect) be optimized. That is, it will still feature $~(m-1)$-nested looping. However, the range of each variable $~y_i~$ will be relatively limited, compared to the strategy in the previous paragraph.

Again assuming that I am not mistaken, this implies that on a vanilla personal computer, you can process significantly larger values of $~(n,m)~$ with the optimized algorithm than with the non-optimized algorithm.

Answer 4

Here is a more intuitive outline for a proof.

• The probability distribution of the sum of cards modulo $n$ has a periodic pattern with length $m$.

  Outline of a proof: compare the sum of cards picked from cards 2 to n+1 and the sum for $m$ cards picked from 1 to n. Note that these cards are the same set modulo $n$. The distribution of the sum will be a shift by $k$. Yet modulo $k$ the distribution must be the same because if we compute a sum modulo $n$ then it doesn't matter when we first compute all the individual terms modulo $k$ (but if we apply modulo $k$ to the cards then we have the same sets). Therefore the distribution must have a cyclic pattern.

  Example from a simulation with $n = 6$ and $m=3$

  

• The probability distribution of the sum of cards modulo $k$ is uniform if $gcd(k,m) = 1$ and $k|n$ and $m|n$.

  For each of the $k$ possible values for the sum modulo $k$, this will correspond to the entire cyclic pattern of length $m$ for which each vakue will be sampled $n/k/m$ times.

  If the sum modulo $k$ equals $p$, then this corresponds to values for sum modulo $n$ of $ik + p$ with $i = 0,1,2\dots, n/k+1$. From these $n/k+1$ values the modulus of $m$ will be encounted the same number of times and it is like the average of the probabilities in the cyclic pattern.

  For example with $n=6,m=3,k=2$ we have if the sum modulo $k=2$ equals $p=0$ the potential sum modulo $n$ values of 0, 2 ,4 and modulo $m=3$ those vakues will be $0,2,1$ which samples the entire cyclic pattern described in the previous point.

Therefore a sufficient condition is

$gcd(k,m) = 1$ and $k|n$ and $m|n$.

and more generally the probability for the sum modulo $k$ is uniform.

---

I believe that another sufficient condition is when $gcd(m,n) = 1$, in that case the distribution for the sum modulo $n$ will be continuous, and so will be the distribution the sum modulo $k$ if $k|n$.