Getting the straight line that passes through the points of tangency of 3 circles

Question

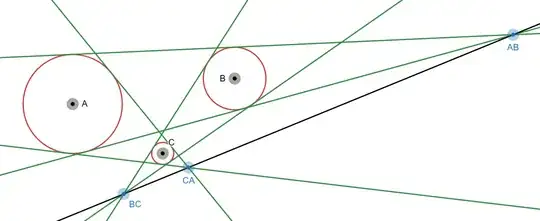
so i was recently interested in monge`s theorem after watching a 3blue1brown video, and wanted to prove that the 3 points are colinear

let 3 circles be

$$ S_1(x,y) \equiv (x-x_1)^2 + (y-y_1)^2 -R_1^2 $$ $$ S_2(x,y) \equiv (x-x_2)^2 + (y-y_2)^2 -R_2^2 $$ $$ S_3(x,y) \equiv (x-x_3)^2 + (y-y_3)^2 -R_3^2 $$ such $A \equiv (x_1, y_1), B \equiv (x_2, y_2), C \equiv(x_3,y_3)$ are the centers of the circles $S_1, S_2, S_3$ and $R_1, R_2, R_3$ are their radii, here $R_1 \not= R_2 \not= R_3$ and neither circles are top of each other

let the intersection point of the common tangent of circle $S_1$ and $S_2$ be at $T_{AB}$ (i used just AB due to desmos not liking subscripts on names of points)

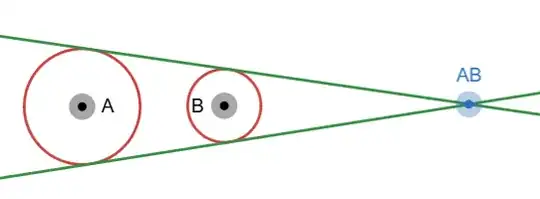
similarly for circle $S_2$ and $S_3$ be at $T_{BC}$ and $S_3$ and $S_1$ be at $T_{CA}$, using similar triangles it can be proven that $$T_{AB}=\left(\frac{R_{1}x_{2}-R_{2}x_{1}}{R_{1}-R_{2}},\frac{R_{1}y_{2}-R_{2}y_{1}}{R_{1}-R_{2}}\right)$$ $$T_{BC}=\left(\frac{R_{2}x_{3}-R_{3}x_{2}}{R_{2}-R_{3}},\frac{R_{2}y_{3}-R_{3}y_{2}}{R_{2}-R_{3}}\right)$$ $$T_{CA}=\left(\frac{R_{3}x_{1}-R_{1}x_{3}}{R_{3}-R_{1}},\frac{R_{3}y_{1}-R_{1}y_{3}}{R_{3}-R_{1}}\right)$$ it can also be proven that point $T_{AB}, T_{BC}, T_{CA}$ are colinear, using equating the gradients, infect monge`s theorem does that

i wanted to get the equation of that colinear line (drawn as the black line in the picture) as (ill use .x and .y as the x and y coordinates of a point as desmos does) $$\frac{y-T_{BC}.y}{x-T_{BC}.x}=\frac{T_{BC}.y-T_{CA}.y}{T_{BC}.x-T_{CA}.x}$$ $$y\left(T_{BC}.x-T_{CA}.x\right)-\left(T_{BC}.y-T_{CA}.y\right)x+\left(T_{CA}.xT_{BC}.y-T_{BC}.xT_{CA}.y\right)=0$$

i had a feeling that this would somehow be simplified into a determinant because usually a lot of similar problems can be solved using determinants for some reason, I've not done linear algebra but this interests me, and wouldn't you know it, it does simplify to a determinant after manipulating variables and cancelling and getting it to a determinant form as $$\left(R_{2}y_{3}-R_{3}y_{2}+R_{1}y_{2}+R_{3}y_{1}-R_{2}y_{1}-R_{1}y_{3}\right)x-\left(R_{2}x_{3}-R_{3}x_{2}+R_{1}x_{2}+R_{3}x_{1}-R_{2}x_{1}-R_{1}x_{3}\right)y+\left(x_{1}y_{2}R_{3}-x_{1}R_{2}y_{3}-y_{1}x_{2}R_{3}+y_{1}R_{2}x_{3}+R_{1}x_{2}y_{3}-R_{1}y_{2}x_{3}\right)=0$$ $$\begin{vmatrix} y_1 & R_1 & 1 \\ y_2 & R_2 & 1 \\ y_3 & R_3 & 1 \end{vmatrix}x- \begin{vmatrix} x_1 & R_1 & 1 \\ x_2 & R_2 & 1 \\ x_3 & R_3 & 1 \end{vmatrix}y- \begin{vmatrix} x_1 & y_1 & R_1 \\ x_2 & y_2 & R_2 \\ x_3 & y_3 & R_3 \end{vmatrix} = 0$$

i`ve seen a similar form on deriving a 4 by 4 matrix to find the circle going thought 3 points as $$\begin{vmatrix} x^2 + y^2 & x & y & 1 \\ x_1^2 + y_1^2 & x_1 & y_1 & 1 \\ x_2^2 + y_2^2 & x_2 & y_2 & 1 \\ x_3^2 + y_3^2 & x_3 & y_3 & 1 \\ \end{vmatrix} = 0 $$ and guessed this can also be shown in a similar 4 by 4 matrix determinant, since maths has a sort of symmetry, so i tried it as $$\begin{vmatrix} x & x_1 & x_2 & x_3 \\ y & y_1 & y_1 & y_3 \\ c & R_1 & R_2 & R_3 \\ 1 & 1 & 1 & 1 \\ \end{vmatrix} = 0 $$

i didn't know what to put as $c$ and just put $0$ in it, and it exactly gave the line, can someone please give an intuitive explanation for why this determinant equaled to $0$ give the colinear tangent points` line? ill put the link for desmos where i did all this just incase https://www.desmos.com/calculator/ux24wicrsr

Answer 1

from the answers i found that just like the 2D equation for the line connecting 2 points which is $$\begin{vmatrix} x & x_1 & x_2 \\ y & y_1 & y_2 \\ 1 & 1 & 1 \end{vmatrix} =0$$ the same is extended for the plane connecting 3 points as $$\begin{vmatrix} x & x_1 & x_2 & x_3 \\ y & y_1 & y_2 & y_3 \\ z & z_1 & z_2 & z_3 \\ 1 & 1 & 1 & 1 \end{vmatrix} =0$$

as above I extended the 3 circles to 3 spheres as $$\left(x-A.x\right)^{2}+\left(y-A.y\right)^{2}+\left(z-R_{1}\right)^{2}=R_{1}^{2}$$ $$\left(x-B.x\right)^{2}+\left(y-B.y\right)^{2}+\left(z-R_{2}\right)^{2}=R_{2}^{2}$$ $$\left(x-C.x\right)^{2}+\left(y-C.y\right)^{2}+\left(z-R_{3}\right)^{2}=R_{3}^{2}$$

with centers $$ P \equiv \left(x_{1},y_{1},R_{1}\right)$$ $$ Q \equiv \left(x_{2},y_{2},R_{2}\right)$$ $$ R \equiv \left(x_{3},y_{3},R_{3}\right)$$

so considering the plane that passes through the given 3 centers as below

$$\begin{vmatrix} x & x_1 & x_2 & x_3 \\ y & y_1 & y_2 & y_3 \\ z & R_1 & R_2 & R_3 \\ 1 & 1 & 1 & 1 \end{vmatrix} =0$$ but since we only need the x,y axis intersection of the plane, we can make the $z=0$ so the plane only exists on the x,y plane as

$$\begin{vmatrix} x & x_1 & x_2 & x_3 \\ y & y_1 & y_2 & y_3 \\ 0 & R_1 & R_2 & R_3 \\ 1 & 1 & 1 & 1 \end{vmatrix} =0$$ thanks for answers btw, I hadn't done linear algebra yet , but this is a still a very interesting field for me.

Answer 2

Consider the "3D analogy" as it is called in the Wikipedia article.

Summarizing the proof one can find there:

The circles are considered as "vertical shadows" of spheres placed on the horizontal plane $\Pi_0$ with centers:

$$(x_k,y_k,R_k) \ \text{for} \ k=1,2,3\tag{1}$$

These spheres have two externaly common tangent planes, one of them being of course horizontal plane $\Pi_0$. The intersection of these planes $\Pi_0 \cap \Pi_1$ is a horizontal line $L$ on which the 3 external homothety centers are lying.

Now let us consider the medial plane $\Pi_2$ passing through the centers ; its equation is (see here), taking (1) into account:

$$\begin{vmatrix} x & x_1 & x_2 & x_3 \\ y & y_1 & y_2 & y_3 \\ z & R_1 & R_2 & R_3 \\ 1 & 1 & 1 & 1 \\ \end{vmatrix} = 0\tag{2}$$

Its intersection with horizontal plane $\Pi_0$ (whose equation is $z=0$) is computed by setting... $z=0$ in (2). It is exactly what you have done !

We have now finished ; indeed, this medial plane $\Pi_2$ being clearly a bissecting plane of $\Pi_0$ and $\Pi_1$, it shares the same line $L$ with them.