2

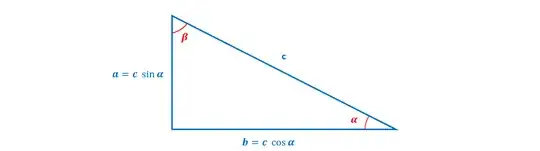
Let $\alpha$ be the angle opposite to side $a$, and $\beta$ be the angle opposite to side $b$, and without loss of generality, assume that $0 < \alpha \leq \beta < 90^\circ$.

We now have:

$$\begin{align} \cos(\beta) &= \cos(\alpha − (\alpha − \beta)) \\ &= \cos(\alpha) \cos(\alpha − \beta) + \sin(\alpha) \sin(\alpha − \beta) \\ &= \cos(\alpha)(\cos(\alpha) \cos(\beta) + \sin(\alpha) \sin(\beta)) + \sin(\alpha)(\sin(\alpha) \cos(\beta) − \cos(\alpha) \sin(\beta)) \\ &= (\cos^2(\alpha) + \sin^2(\alpha)) \cos(\beta), \end{align}$$

from which it follows that $\cos^2(\alpha) + \sin^2(\alpha) = 1$, since $\cos(\beta)$ is the ratio between one leg and the hypotenuse of a right triangle, and as such is never zero. The theorem now follows from the definitions of sine and cosine and scaling.

I am not sure if I am understanding the proof correctly; I have trouble getting what the "scaling" means and why it is necessary.

M. A.
  • 1,774
Hjm
  • 71
  • 1
    Please do not use pictures for critical portions of your post. Pictures may not be legible, cannot be searched and are not view-able to some, such as those who use screen readers. – Another User Oct 18 '24 at 16:33
  • 2
    Dividing by the hypotenuse is the scaling factor. That way you can reduce all similar right triangles to ones that have a point on the unit circle. – CyclotomicField Oct 18 '24 at 16:47
  • 2
    Personally, I think that the entire approach is invalid. Formulas for $~\sin(\alpha + \beta)~$ and $~\cos(\alpha + \beta)~$ were derived using the Pythagorean theorem as a premise. Therefore, attempting to use these formulas to then prove the Pythagorean theorem is circular reasoning. – user2661923 Oct 18 '24 at 17:06
  • 1
    Certainly it's healthy to be wary of circular reasoning in arguments like this, but there are definitely ways to derive the sum of angle formulas that do not rely on the Pythagorean theorem. – Jakob Streipel Oct 18 '24 at 17:21
  • @CyclotomicField can you give a more detailed answer? I get that dividing the sides by the hypotenuse transforms the right triangles into triangles that fit within the unit circle, but why do I need that? I can't use the definition of sin and cos without it? – Hjm Oct 18 '24 at 17:37
  • You're trying to prove something about the sides of an arbitrary right-angle triangle. You have to relate, somehow, the problem about triangles to the trig identity. Scaling is what does the relating for you. – Gerry Myerson Oct 19 '24 at 08:32
  • @GerryMyerson I thought the definitions of sine and cosine did that relating – Hjm Oct 19 '24 at 09:20
  • 1
    @user2661923: "Formulas for $\sin(\alpha+\beta)$ and $\cos(\alpha+\beta)$ were derived using the Pythagorean theorem as a premise." Not necessarily. See, for instance, this old answer of mine, showing a diagrammatic proof of the formulas, wherein sines and cosines are effectively only shorthand names for ratios of lengths in a right triangle. At no time is the Pythagorean property itself invoked. – Blue Oct 19 '24 at 10:39
  • You have to relate numbers of arbitrary size to numbers that are at most one. You do that by scaling, Hjm. – Gerry Myerson Oct 19 '24 at 11:25
  • The scaling precisely introduces a circularity in the proof. Because the sides are $a$ and $b$ instead of cosine and sine, and you need to multiply by the length of the hypothenuses, which is $\sqrt{a^2+b^2}$... if the Pythagorean theorem holds. –  Oct 24 '24 at 20:59

3 Answers3

3

The proof you mentioned showed that for any $\alpha\in\left(0,\frac\pi2\right)$, $$ \cos^2\alpha+\sin^2\alpha=1 $$ Therefore, for any $l>0$, $$ (l\cos\alpha)^2+(l\sin\alpha)^2=l^2 $$ This process is called scaling. Consider a rectangular triangle. Let an acute angle of it be $\alpha$, then $l\cos \alpha$ and $l\sin\alpha$ are the side lengths of the rectangular sides, and $l$ is the length of the longest side. Since $\alpha$ is arbitrary, Pythagoreion theorem is proved.

Note. There is no circular reasoning here, as we can deduce formulas for things like $\cos(\alpha+\beta)$ without using Pythagoreion theorem. Consider the following rectangle. (In the picture $\gamma=\alpha+\beta$) enter image description here

Here we have $$ \begin{align} \cos(\alpha+\beta)=\frac ah&&\cos\alpha=\frac{a+b}g&&\cos\beta=\frac gh&&\sin\alpha=\frac eg&&\sin\beta&=\frac dh \end{align} $$ Therefore, $$ \cos\alpha\cos\beta-\sin\alpha\sin\beta=\frac{a+b}h-\frac eg\cdot\frac dh=\frac{a+b}h-\frac bh=\frac ah=\cos(\alpha+\beta) $$ Since by triangular similarity $\frac dg=\frac be$.

Nuaptan
  • 153
0

Trigonometric constructions are based on the Pythagorean theorem, and we have a big chances to get incorrect proof. However, we can try to use an idea of the trigonometrical circle.

The set of possible third vertices $\;B(x,y)\;$ of the right triangle with the given vertices $A(-R,0)$ and $C(R,0)$ can be calculated from the condition $$\overrightarrow{AB} \perp \overrightarrow{BC} \Rightarrow \{x+R,y\}.\{R-x, -y\}=0,$$ or $$R^2-x^2-y^2=0.$$

On the other hand, $R$ is the hypotenuse of the right triangle OBX with the legs $OX=x$ and $XB=y.$

Pythagor

Proved!

Yuri Negometyanov
  • 28,835
0

With reference to the following sketch

enter image description here

from what you have already shown, we obtain

$$\cos^2 \alpha + \sin^2 \alpha =1 \implies c^2\cos^2 \alpha + c^2\sin^2 \alpha =c^2 \implies \boxed{a^2+b^2=c^2}$$

user
  • 162,563