3

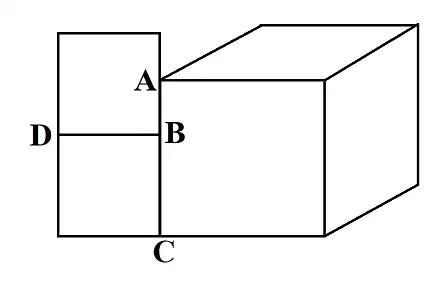
Two identical squares were attached to the edge of a cube.

Given:

$$ \text{AB} \cdot \text{BC} = 8.5 \\ \text{AD} = \sqrt{8} $$

What is the volume of the cube?

The question visually

My straight-forward answer:

Having:

$$ \text{AD} = \sqrt{8} \\ \text{AB} = x \\ \text{BC} = y \\ x \cdot y = 8.5 $$

We have two equations:

$$ x^2 + y^2 = \left( \sqrt{8} \right )^2 = 8 \\ x \cdot y = 8.5 \iff 2xy = 17 $$

Thus adding both together:

$$ x^2 + y^2 + 2xy = \left ( x + y \right )^2 = 17 + 8 = 25 \\ x + y = 5 $$

And the volume is $ (x+y)^3 $ thus it's $5^3 = 125$

The post-answer question

Ok, having the answer that each edge is equal to 5 I wanted to find the exact values of $x$ and $y$, we know from the previous answer that $x+y = 5$, so we can have this system of equations:

$$ \left\{\begin{matrix} xy = 8.5 & \\ x+y = 5& \\ \end{matrix}\right. $$

This simplified down to this equation:

$$ y = \frac{8.5}{x} \\ x + \frac{8.5}{x} = 5 \\ x^2 + 8.5 = 5x \\ x^2 - 5x + 8.5 = 0 $$

Which doesn't yield any real solutions for $x$ thus neither not for $y$.

My question is simple - what am I doing wrong here? I am surely missing something, thanks!

0Interest
  • 2,809

1 Answers1

2

The original data given is wrong. Assuming that is originally correct, you should arrive at

$$(x+y) = 5 \qquad \text{and} \qquad (xy) = 8.5.$$

You did this much correctly. Now, looking at this, we see there can't be any solution to this equation. The maximum product that can be achieved from $x$ and $y$ is $6.25$, obtained by setting each of them as $2.5$.

To prove this, plot the graph of $x(5-x)$, which is essentially the graph of $xy$; you will see it has its vertex at $(2.5, 6.25)$.

Hence, $x$ and $y$ can't have a product of $8.25$, implying that the original given data is wrong.

M. A.
  • 1,774
Aarav Agarwal
  • 56