0

Does the following smooth function have any non-zero points where it is analytical (real-valued meaning)? (Fabius function's lobe lookalike)

In a previous question I made a smooth bump function with straight-line at the slopes, defined by: $$h(x)=\int\limits_{-1}^{x}f(y) \, \mathrm{d}y$$ with its argument defined as: $$f(x) = \begin{cases} 0,\quad |x|\geq 1\\ 0,\quad x= 0\\ 2,\quad x=-\frac12\\ -2,\quad x=\frac12\\ \dfrac{-2\,\text{sgn}(x)}{1+\exp\left(\frac{1-2||2x|-1|}{(|2x|-1)^2-||2x|-1|}\right)},\quad\text{otherwise} \end{cases}$$

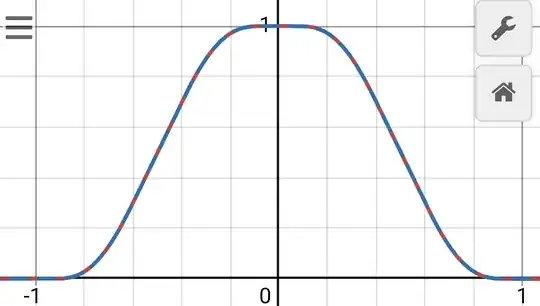
which I already know is smooth but not analytical at point $x=\{-1,\ 0,\ 1\}$ by construction since it is a flat function there also I think it isn't analytical at points $x=\left\{-\frac12,\ \frac12\right\}$ since the first derivative is a flat function there, which will give just a constant value in the power series when it's trying to fit the equation of a line with slope different from zero.

But looking at its plot, it resembles very close to the lobes of the Fabius function, which Wikipedia describes as "an example of an infinitely differentiable function that is nowhere analytic", and I am wondering if accidentally I found something with the same property. So far, I have not been able to use Wolfram-Alpha to verify the Taylor series at any point, neither for it's derivative (I found the function using Wolfram-Alpha and a comment done by user @mattTheMathLearner on the previous question).

Here is a Desmos plot of the function $h(x)$ compared with an approximation of a displaced version of the lobes of the Fabius function.

match between approximations

Could you find any points $x$ where $h(x)\neq 0$ it is analytical? (meaning here h(x) matches with his Taylor's expansion)

Update 1: Attempt 1

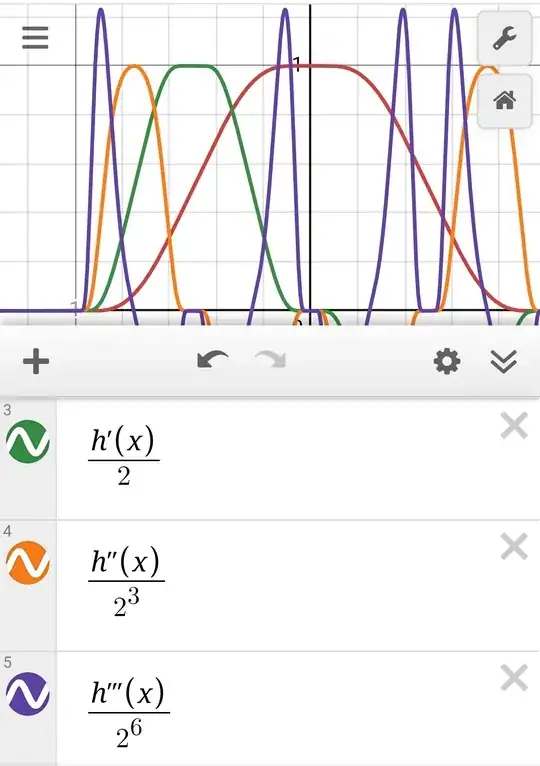
I plot the derivatives $h'(x)$, $h''(x)$, and $h^{(3)}(x)$ in Desmos and from the second one the funcrtions stop having flat sections, so in principle, in the parts the function $h(x)$ its curvy the coefficients of the Taylor's expansions should't become zero after some finite summation index, so I think there are Taylor's series associated to those points. What remains to be proven if these Taylor's series are converging to $h(x)$.

derivatives of h(x)

Joako
  • 1,957

1 Answers1

1

$f$ is definitely analytic in $\mathbb R\setminus \{-1,-1/2,0,1/2,1\}$, since you can rewrite it in each interval as a composition of analytic functions (exponential, power, fraction,…). A primitive of an analytic function on $\mathbb R$ is also analytic (you can write the ansatz of the power series explicitly by taking the primitive of each monomial, check that the series converges, and that differentiating it yields the original function), so $h$ is analytic on the same domain.

Lorenzo Pompili
  • 5,569
  • thanks for the answer. I was not able to find the monomials since the derivatives are spitting out Dirac's Delta functions from the sign function and the absolutes values... How you will compute those monomials? – Joako Oct 15 '24 at 18:58
  • 1
    If you restrict the function $f$ on, say, the interval $(1/2,1)$, you can remove all the absolute values and sign without changing the function, and carry the computations more easily. For the other intervals, you can do the same by putting appropriate signs in front of the arguments of the absolute values. This w ay you can compute explicitly all the derivatives of $f$. For $h$, if $f(x)=\sum_{n\geq 0} a_n(x-x_0)^n$ on some neighbourhood of $x_0$, then $h(x)=\sum_{n\geq 0} \frac{a_n}{n+1}(x-x_0)^{n+1}+c$, for some constant $c$. – Lorenzo Pompili Oct 15 '24 at 19:03
  • mmm... let me see if I followed you: as example to valuate analyticity on the point $x=-0.1$ then I should replace $$h'(x) \equiv g(x)=\dfrac{1}{1+\exp\left(\dfrac{1-2(2x+1)}{(2x+1)^2-(2x+1)}\right)}$$ and then evaluate the Taylor's series for $g(x)$ $$T_g(x)=1+\frac{1}{2x}-\frac{1}{8x^2}+O(x^3)$$, this is right? – Joako Oct 15 '24 at 19:15
  • 1
    Yes, it looks correct – Lorenzo Pompili Oct 15 '24 at 19:53
  • Thanks, I didn't know it was valid to replace by equivalent function by intervals ir order to evaluate anlyticity – Joako Oct 15 '24 at 20:08