Very interesting problem indeed! It is late at night, so I apologise in advance for any typo :)
Let' consider (just to note that we start summation from $k=0$)
$$S=\sum_{k=0}^n\left(1+t\sin\frac{2\pi k}n\right)^{-\alpha}$$
where we chose for a while $0<\alpha<1$
In a standart way, switching to complex integration
$$2\pi iS=\pi t^{-\alpha}\oint_C\cot\pi z\left(\frac1t+\sin\frac{2\pi z}n\right)^{-\alpha}dz=\pi t^{-\alpha}\oint_C\cot\pi z\left(\cosh\frac{2\pi s_0}n+\sin\frac{2\pi z}n\right)^{-\alpha}dz$$
where $\,s_0=\frac{n}{2\pi}\operatorname{arch}\frac1t=\frac{n}{2\pi}\ln\left(\frac1t+\sqrt{\frac1{t^2}-1}\right)$, and the contour $C$ embraces the points $z=0,1,2,...n,\,$ . As we have two branch points $z=\frac{3n}4\pm is_0$, we deform the contour and integrate along the following way (adding two cuts and keeping the integrand an analytical function)
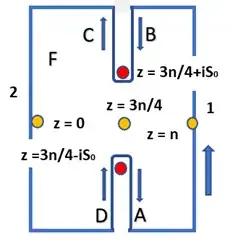
Integrals along the paths 1 and 2 cancel each other; at $z\to\pm i\infty$ the integrand declines exponentially, so the integral along the horizontal paths tend to zero, and we are left with the integrals along the paths A,B,C,D (and, of course, the half-residues at the points $z=0, n$)
Hence,
$$2\pi iS=2\pi i+I_A+I_B+I_C+I_D$$
Appointing the phases to the paths at $z\to\pm i\infty$, and taking into account the change of phases while turning around the branch points
$$2\pi iS=2\pi i-\frac{1-e^{2\pi i\alpha}}{e^{\pi i \alpha}}\pi t^{-\alpha}i\int_{s_0}^\infty\cot\pi\big(\frac{3n}4-is\big)\left(\cosh\frac{2\pi s}n-\cosh\frac{2\pi s_0}n\right)^{-\alpha}ds$$
$$+\frac{1-e^{-2\pi i\alpha}}{e^{-\pi i\alpha}}\pi t^{-\alpha}i\int_{s_0}^\infty\cot\pi\big(\frac{3n}4+is\big)\left(\cosh\frac{2\pi s}n-\cosh\frac{2\pi s_0}n\right)^{-\alpha}ds$$
Given that $n\gg1\,\,s_0\gg1$, and we can decompose $\cot$ near this point (just to mention that such decomposition allows to get full asymptotics). Keeping only two terms,
$$\approx 2\pi i+4i\sin(\pi\alpha)\,\pi t^{-\alpha}\int_{s_0}^\infty\left(1+\cos\frac{3\pi n}2e^{-2\pi s}\right)\left(\cosh\frac{2\pi s}n-\cosh\frac{2\pi s_0}n\right)^{-\alpha}ds$$
$$=2\pi i+4i\sin(\pi\alpha)\,\pi t^{-\alpha}(I_1+I_2)$$
To evaluate $I_2$, we use again the condition $n\gg1$:
$$\int_{s_0}^\infty e^{-2\pi s}\left(\cosh\frac{2\pi s}n-\cosh\frac{2\pi s_0}n\right)^{-\alpha}ds\approx e^{-2\pi s_0}\int_0^\infty e^{-2\pi s}\left(\sinh\big(\frac{2\pi s_0}n\big)\,\frac{2\pi}ns\right)^{-\alpha}ds$$
$$=e^{-2\pi s_0}\left(\sinh\big(\frac{2\pi s_0}n\big)\right)^{-\alpha}\frac{n^\alpha}{2\pi}\Gamma(1+\alpha)$$
To evaluate $I_1$, we make the following transformations:
$$\int_{s_0}^\infty\left(\cosh\frac{2\pi s}n-\cosh\frac{2\pi s_0}n\right)^{-\alpha}ds=\frac n{2\pi}\int_{\operatorname{arch\frac1t}}^\infty\left(\cosh x-\frac1t\right)^{-\alpha}dx$$
$$=\frac n{2\pi}\int_{\frac1t}^\infty\frac{\big(x-\frac1t\big)^{-\alpha}}{\sqrt{x^2-1}}dx=\frac{nt^\alpha}{2\pi}\int_0^1\frac{(1-x)^{-\alpha}x^{\alpha-1}}{\sqrt{1-t^2x^2}}dx$$
But
$$\sin\pi\alpha\int_0^1\frac{(1-x)^{-\alpha}x^{\alpha-1}}{\sqrt{1-t^2x^2}}dx=\pi\int_0^1\left(1+t\sin(2\pi x)\right)^{-\alpha}dx$$
I leave this to be rigorously proved by those who are interested; myself, check via decomposition and integration term by term (and confirmed numerically).
So, taking all together, we get the answer:
$$S=\sum_{k=0}^n\left(1+t\sin\frac{2\pi k}n\right)^{-\alpha}\approx 1+n\int_0^1\big(1+t\sin(2\pi x)\big)^{-\alpha}dx$$
$$+t^{-\alpha}\sin(\pi\alpha)\cos\frac{3\pi n}2n^\alpha e^{-2\pi s_0}\sinh^{-\alpha}\left(\frac{2\pi s_0}n\right)\Gamma(1+\alpha);\,\,\alpha\in(0,1)$$
Implementing analytical continuation, we can consider any real $\alpha$. For example, taking $\alpha=-\frac12$ we get the asymptotic that I mentioned in the comment (and that initially found by not rigorous way). Just expressing $s_0$ via $ n, t$
$$\sum_{k=1}^n\left(1+t\sin\frac{2\pi k}n\right)^{\frac12}\sim n\int_0^1\big(1+t\sin(2\pi x)\big)^\frac12dx-\frac{\cos\frac{3\pi n}2}{\sqrt{\pi n}}(1-t^2)^{\frac14}\left(\frac{1+\sqrt{1-t^2}}t\right)^{-n}$$
In the case of odd $n$ we have to consider next terms of the decomposition of $\cot\big(\frac{3\pi}4\pm is\big)$ to find non-zero asymptotic terms.
Numeric checks with WA confirm the result (just one point: you have to evaluate $\,\sum_{k=1}^n\left(1+t\sin\frac{2\pi k}n\right)^{\frac12}\,$ and $\,n\int_0^1\big(1+t\sin(2\pi x)\big)^\frac12\,$ numerically separately, and only then take the difference. If you put $\,\sum_{k=1}^n\left(1+t\sin\frac{2\pi k}n\right)^{\frac12}-n\int_0^1\big(1+t\sin(2\pi x)\big)^\frac12\,$ in WA, the number may be not correct. These are bugs of WA free option.)
There is also a more rich case of alternating series (I also mentioned it in the comment). Using complex integration we can get, for example,
$$\sum_{k=0}^n(-1)^k\sqrt{1+t\sin\frac{2\pi k}n}\sim\frac{1+(-1)^n}2+\big((-1)^n-1\big)\frac{\pi t}{4n}\left(1+O\Big(\frac 1{n^2}\Big)\right)$$
$$-\,\sqrt{\frac 8{\pi n}}\cos\frac{3\pi n}4(1-t^2)^\frac14\left(\frac{1+\sqrt{1+t^2}}t\right)^{-\frac n2}$$
Here I keep the exponentially small term just to show that it contributes at even $n$
