0

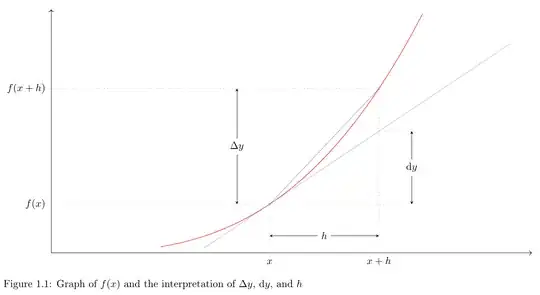
Let $f(x)$ be an arbitrary function, as shown in the figure below (Figure 1.1).

  1. When $x$ increases by $h$, the change in $y$ is straightforward: $$ \Delta y = f(x+h) - f(x). $$

  2. The average rate of change with respect to $h$ (where $h \neq 0$) is given by: $$ \frac{\Delta y}{h} = \frac{f(x+h) - f(x)}{h}. $$

So far, this makes sense to me.

Now, I'm struggling with two things:

First:

I understand that Leibniz's notation, $\frac{dy}{dx}$, is just that — a notation. What it represents is the limit: $$ \lim\limits_{h \to 0} \frac{f(x+h) - f(x)}{h}. $$ But what about $dy$? Is $dy$ also "just" a notation, or does it have a different meaning? My interpretation is that: $$ dy = \left\{\lim\limits_{h\to 0}\frac{f(x+h) - f(x)}{h} \right\} \cdot dx. $$ Is this correct?

Second:

Using Leibniz's notation, I could write: $$ dy = \frac{dy}{dx} \cdot dx. $$ However, this form contains two identical $dx$ symbols. One is in the denominator of $\frac{dy}{dx}$ (which is part of Leibniz's notation and doesn’t represent anything specific), and the other $dx$ represents the step in $x$. In this context, $dx = h$. This confuses me because both are written the same, but seem to mean different things. Can someone explain how to interpret these two $dx$ symbols correctly?

enter image description here

Marco Moldenhauer
  • 129
  • see https://math.stackexchange.com/questions/143222/what-does-dx-mean – Horned Sphere Sep 12 '24 at 03:42
  • 1
    $\Delta$y is the vertical distance between the y-coordinates of the two points on the function graph, while dy is the vertical distance between the y-coordinate of the first point and the y-coordinate the line tangent to the first point passes through after the same horizontal distance, as your graph shows. – Nate Sep 12 '24 at 03:46
  • 3
    This question has the most duplicates on MSE. Here is one: What does $dx$ mean?. – Kurt G. Sep 12 '24 at 05:16
  • 1
    For your first question, the answer is NO. A limit does not, and cannot, represent an infinitesimal. (The concept of a limit is designed specifically to eliminate infinitesimals, leaving only definite values.) Regarding your second question, you are correct that $\frac{\mathrm{d}y}{\mathrm{d}x}$ is not a typical fraction but rather an inseparable entity of its own. You are also correct that the standalone $\mathrm{d}x$ must be defined independently of Leibniz's notation, which can indeed be accomplished with full mathematical rigor but requires a certain level of mathematical maturity. – Sangchul Lee Sep 12 '24 at 11:58
  • @SangchulLee thanks a lot fr you anser. Ok thanks for answering question 2. This is ok for me now. But regarding question 1. you wrote " A limit does not, and cannot, represent an infinitesimal". but I wrote "$dy = \left{\lim\limits_{h\to 0}\frac{f(x+h) - f(x)}{h} \right} \cdot dx$" there is also this $dx$ as factor on the right hand side and the on the left hand side there is the limit $\lim\limits_{h\to 0}\frac{f(x+h) - f(x)}{h}$ which means in Leibnitz notation $dy/dx$, so $dy = \left{\lim\limits_{h\to 0}\frac{f(x+h) - f(x)}{h} \right} \cdot dx$ is not correct? thx and best regards – Marco Moldenhauer Sep 13 '24 at 05:08
  • 1
    @MarcoMoldenhauer, Ah, I see that now. Somehow I failed to notice the factor $\mathrm{d}x$ in the right-hand side. That makes sense. :) – Sangchul Lee Sep 13 '24 at 05:26

0 Answers0