Hands-on calculation of the number of collisions in hashing

Question

Consider the problem from Introduction to Algorithms by Cormen et. al below:

Suppose we use a hash function h to hash n distinct keys into an array T of length m . Assuming simple uniform hashing, what is the expected number of collisions? More precisely, what is the expected cardinality of {{k,l}:k≠l and h(k)=h(l)} ?

This question has been asked in multiple forms - and answered - multiple times (1, 2, 3, 4) and the correct result is $\frac{n(n−1)}{2m}$.

What I'm after is to actually "see" how that final number comes to be. For this I'm running the problem with low values of m and n. I'm also thinking of balls and bins to picture the whole thing, as at least for me it makes it less abstract. To get all the possible combinations of the balls landing into bins I use the idea from this video where we can simplify the problem by considering all possible permutations of m letters B (B for "ball") and a divider sign (separator between bins, so there will be m-1 such signs).

Finally I count the number of collisions - make sure to take into account the actual definition of "collision" for this problem (e.g. one new ball dropping into a bin with 3 existing balls will result in 3 collisions, then a new ball placed in the same bin will generate 3 more collisions, etc). I then divide the number of overall collisions found when generating all possible permutations by the number of permutations themselves, and get the average number of collisions.

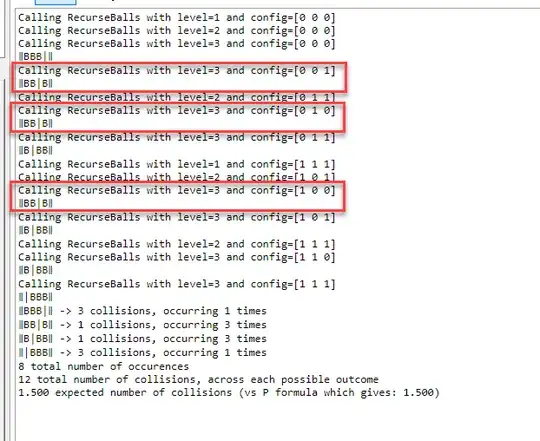
For 3 balls and 2 bins I get (whereby the correct formula gives $\frac{6}{4}=1.5$)

∥BBB|∥ -> 3 collisions
∥BB|B∥ -> 1 collisions
∥B|BB∥ -> 1 collisions
∥|BBB∥ -> 3 collisions
4 combinations found
2 average collisions (8 overall collisions / 4 combinations)

For 5 balls and 3 bins we get (whereby the correct formula gives $\frac{20}{6}=3.333$)

∥BBBBB||∥ -> 10 collisions
∥BBBB|B|∥ -> 6 collisions
∥BBBB||B∥ -> 6 collisions
∥BBB|BB|∥ -> 6 collisions
∥BBB|B|B∥ -> 3 collisions
∥BBB||BB∥ -> 6 collisions
∥BB|BBB|∥ -> 6 collisions
∥BB|BB|B∥ -> 3 collisions
∥BB|B|BB∥ -> 3 collisions
∥BB||BBB∥ -> 6 collisions
∥B|BBBB|∥ -> 6 collisions
∥B|BBB|B∥ -> 3 collisions
∥B|BB|BB∥ -> 3 collisions
∥B|B|BBB∥ -> 3 collisions
∥B||BBBB∥ -> 6 collisions
∥|BBBBB|∥ -> 10 collisions
∥|BBBB|B∥ -> 6 collisions
∥|BBB|BB∥ -> 6 collisions
∥|BB|BBB∥ -> 6 collisions
∥|B|BBBB∥ -> 6 collisions
∥||BBBBB∥ -> 10 collisions
21 combinations found
5.714286 average collisions (120 overall collisions / 21 combinations)

Simulations for higher values of m and n show the same pattern: the number of collisions I compute is always higher than the correct answer.

My question is simply what am I doing wrong?

Answer 1

The major mistake I was doing - as pointed out very well by @KurtG. - is to consider that each possible balls-in-bins configuration happens only once. Let's look at this below.

For the scenario with 3 balls and 2 bins, each ball that's dropped can either go to the first bin or the second one. For all 3 balls to land in the first bin (configuration BBB|), all 3 balls have to "land" just right, in the first bin. We can't have any of the 3 balls land by chance in the second bin.

But for 2 balls to land in the first bin and one ball to land in the second bin (configuration BB|B) there are more ways to get there, as depicted below. And to generate all the possible combinations, it's actually better to stay away from just generating the end state permutations (as I did in my original post) and actually go through each possible end state that the balls can "land in". We actually want to see all the end states that repeat themselves, as we'll count those later on.

The config values simply tell the bin in which the balls end up. The first possibility highlighted to get to BB|B is to have the first ball dropping in the first bin, then the second one in the first bin also, and the third one in the second bin. Yet if the second ball drops by chance in the second bin instead, we can still get to our target end state BB|B should the third ball also happens to land in the first bin - which is what we see in the second highlight. Yet a third possibility is that the first ball goes in the second bin, and the second and third balls go into the first bin.

So regardless if the first ball lands in either the first or second bin, we can still have chances to get to our end state of BB|B just fine. We don't have this luxury with the BBB| configuration - if any of the balls land in the second bin it's game over.

Once we have the number of occurrences that each end state shows up, we can proceed to compute the total number of collisions encountered across all of them. But we need to be "fair" and count the number of collisions for an end state across each such occurence. So for BB|B we'll add the number of collisions this generates (1, as there's a single one happening) and multiply it by the number of its occurrences (3, as we've seen above).

Next we need the total number of possible end states. We can either count them, or spot that it's quite easy to compute: each ball cand land into one bin, so each number in the config variable will be between 0 and m-1. There are n balls overall, so config contains n such numbers. Therefore the number for all the possibilities for the config variable is $n^m$.

We then divide the "weighted sum" of the number of collisions by the total number of occurrences for each end state, and we get the expected number of collisions. This value will match the $\frac{n(n-1)}{2m}$ formula.

There was a second small issue in my OP, whereby my code was sometimes wrongly counting the number of collisions. E.g for BB|B|BB there are 2 collisions happening, not 3 as stated initially.

The correct outcome below for the 5 balls and 3 bins case:

Partial relevant output for the case with 7 balls and 4 bins: