Is sudoku only one puzzle?

Question

Consider a graph G where each node represents a possible Sudoku solution. We define edges between nodes based on the application of specific "equivalent transformations" that map one solution to another. These transformations include:

1. relabeling numbers;
2. reflection;
3. rotation;
4. permutation of blocks of columns (1-3, 4-6, 7-9);
5. permutation of blocks of rows (1-3, 4-6, 7-9);
6. permutation of columns within each block (1-3, 4-6, 7-9) and
7. permutation of rows within each block (1-3, 4-6, 7-9).

So: an edge is drawn between two nodes if one solution can be transformed into the other by applying any of these transformations.

Given this construction, is the resulting graph G connected? In other words, is there a path between any two nodes in the graph?

Answer 1

No, it is not the case. In the comments, Thomas Andrews suggests an invariant: for $1\leq i<j\leq 9$, define $T_{i,j}$ as the number of rows and columns such that $i,j$ are in the same third. The multiset consisting of all the $T_{i,j}$ values does not change under any of the listed symmetries. Because of this, we get a negative answer so long as we find two puzzles which differ under this invariant. Below are two explicit puzzles which differ in that way.

It's very easy to verify this sudoku, since each block is practically identical under translation. In this first puzzle, we can see that for any two numbers $i\neq j$, we either have $i$ and $j$ in the same third for all $9$ blocks, or else we never have $i,j$ in the same third of any block whatsoever. Using the invariant established previously, we see $T_{i,j}\in\{0,9\}$ for all $i,j$, and so the multiset of all the $T_{i,j}$ values doesn't contain any numbers besides $0$s and $9$s. The following puzzle violates this rule.

In the above puzzle, we can see that $1,7$ are in the same third in the top left block, but not in the middle block, so in particular $T_{1,7}\notin \{0,9\}$. If you're concerned about verifying this sudoku, you can use practically any solved puzzle to replace this second example. Most solved puzzles aren't nearly as organized as my first example.

Answer 2

According to Wikipedia, for classical Sudoku, the number of validly filled grids is $6{,}670{,}903{,}752{,}021{,}072{,}936{,}960 \approx6.671×10^{21}$, which reduces to $5{,}472{,}730{,}538$ essentially different solutions under the equivalence transformations.

A direct reference for this is the 2006 paper of Russell & Jarvis.

Answer 3

There two are different:

The first one has no rectangle with only two values.
The second one has rectangles with only two values (highlighted in yellow).
By rectangle I mean the intersection of two rows and two columns.

Answer 4

This answer is very similar to the one by @JadeVanadium (+1), but with explicit Sudoku solutions and verification, replaced by constructions and argument. I think it is nice to have both.

A completed Sudoku is precisely a function $f\colon {\mathbb{F}_3}^4\to {\mathbb{F}_3}^2$ satisfying that for any $a_1,a_2,a_3,a_4\in {\mathbb{F}_3}$ the following maps are bijections:

$$ (x,y)\mapsto f(x,y,a_3,a_4),\\(x,y)\mapsto f(a_1,a_2,x,y),\\(x,y)\mapsto f(x,a_2,y,a_4). $$

These three conditions are just the usual restrictions that rows, columns, and blocks contain distinct entries.

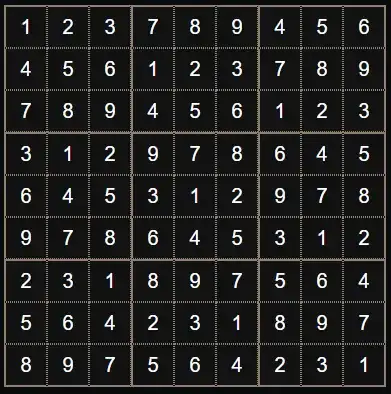
Thus one solution is $f(a_1,a_2,a_3,a_4)=(a_1+a_4,a_2+a_3)$.

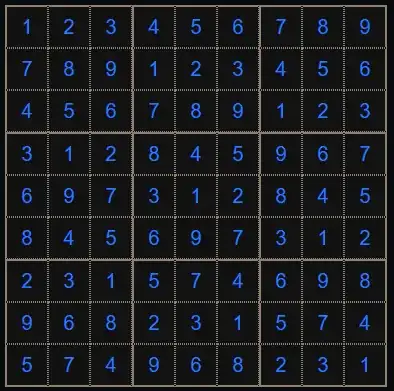
This generalises to the family of solutions $f^\lhd(a_1,a_2,a_3,a_4)=(a_1+a_4,(a_1\lhd a_2)+a_3)$ where for $i\in \mathbb{F}_3$, we have $i\lhd \in S_{\mathbb{F}_3}$.

Let $C$ be the set of $54$ lines in ${\mathbb{F}_3}^4$ the form $(*,a_2,a_3,a_4)$ or $(a_1,a_2,*,a_4)$ (where the $a_i$ are fixed values). For a completed Sudoku $h$, let $N(h)$ denote the number of distinct images of elements of $C$: $$N(h)=|\{h(I)\subset {\mathbb{F}_3}^2\vert\,\, I\in C\}|.$$

Transformation 1 will relabel the images $h(I)$, but not change the number of them. We claim the remaining transformations permute the elements of $C$, so also do not effect $N(h)$:

Transformation 2 consists of maps of the form $$\qquad\,\,\,\,(a_1,a_2,a_3,a_4) \mapsto (-a_1,-a_2,a_3,a_4)\\{\rm or}\qquad (a_1,a_2,a_3,a_4) \mapsto (a_1,a_2,-a_3,-a_4) $$

These clearly preserve elements of $C$.

Transformation 3 consists of maps of the form $$\qquad\,\,\,\,(a_1,a_2,a_3,a_4) \mapsto (a_3,a_4,-a_1,-a_2)\\{\rm or}\qquad\qquad (a_1,a_2,a_3,a_4) \mapsto (-a_3,-a_4,a_1,a_2)\\{\rm or}\qquad (a_1,a_2,a_3,a_4) \mapsto (-a_1,-a_2,-a_3,-a_4)\,\,\, $$

These also preserve elements of $C$, with the first two interchanging the lines of the form $(*,a_2,a_3,a_4)$ with the lines of the form $(a_1,a_2,*,a_4)$.

Transformations 4 and 5 have the form:$$\qquad\,\,\,\,(a_1,a_2,a_3,a_4) \mapsto (a_1,\sigma(a_2),a_3,a_4)\\{\rm or}\qquad (a_1,a_2,a_3,a_4) \mapsto (a_1,a_2,a_3,\sigma(a_4)) $$

respectively, for some $\sigma\in S_{\mathbb{F}_3}$. Clearly these also preserve elements of $C$.

Transformations 6 and 7 have the form:$$\qquad\,\,\,\,(a_1,a_2,a_3,a_4) \mapsto (\sigma_{a_2}(a_1),a_2,a_3,a_4)\\{\rm or}\qquad (a_1,a_2,a_3,a_4) \mapsto (a_1,a_2,\sigma_{a_4}(a_3),a_4) $$ respectively, for $\sigma_i\in S_{\mathbb{F}_3}$ which depend on the parameter $i$. These preserve elements of $C$. Note these make a complete mess of lines of the form, $(a_1,*,a_3,a_4)$ or $(a_1,a_2,a_3,*)$, which is why we defined $C$ the way we did.

We conclude that $N$ is invariant on equivalence classes of completed Sudoku's.

Now $N(f)= 6$, as the images of elements of $C$ under $f$ are just the horizontal or vertical lines in ${\mathbb{F}_3}^2$.

It remains to find a product $ \lhd\colon \mathbb{F}_3 \times \mathbb{F_3} \to \mathbb{F_3}$ such that $N(f^\lhd)\neq 6$. Recall, the only constraint we placed on $\lhd$ in order for $f^\lhd$ to be a valid Sudoku solution was for $i\in \mathbb{F}_3$, we have $i\lhd \in S_{\mathbb{F}_3}$.

Thus $$i\lhd j = (-1)^{\delta_{0i}}j,$$ gives us a valid Sudoku solution $f^\lhd$, where $\delta$ is the usual Kronecker delta.

The lines $(a_1,a_2,*,a_4)$ map to the $3$ vertical lines in ${\mathbb{F}_3}^2$ just as they did under $f$. Also the lines $(*,0,a_3,a_4)$ map to the same $3$ horizontal lines as they did under $f$. However $(*,1,0,0)$ maps to the set: $$\{(0,2),(1,1),(2,1)\}.$$ This is neither a vertical nor horizontal line, so we have $N(f^\lhd)>6$. Thus $f$ and $f^\lhd$ are nonequivalent Sudoku solutions. (In fact it is easy to see that the $18$ elements of $C$ which do not map to horizontal or vertical lines all map to distinct images in ${\mathbb{F}_3}^2$, so $N(f^\lhd)=24$).

In conventional Sudoku terms, $f$ is essentially the first solution in Jade Vanadium's answer, and we obtain $f^\lhd$ from $f$ by swapping the 2nd and 7th columns. This transformation does not in general preserve solutions, but it does in this case because $f$ has so much symmetry. The set $C$ is just the set of thirds, so the invariant $N$ is very similar to the one in Jade Vanadium's answer. In fact it is clear that if you swap the 1st and 4th columns in Jade Vanadium's first solution, then the pair $1,2$ will occur in the same third in precisely $5\notin\{0,9\}$ of the boxes.