Symmetry group structure of frieze pattern $\mathrm{p1m1}$

Question

Context

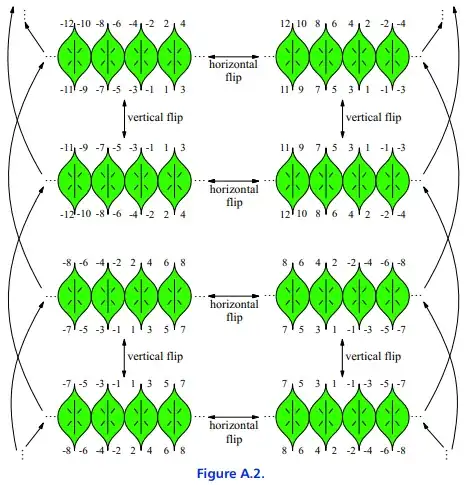
I was reading about frieze groups in Nathan Carter's Visual Group Theory. On page 263, in the answer to Exercise 3.11, the author describes the frieze pattern $\mathrm{p2mm}$, with the corresponding figure $\mathrm{A2}$ given on the next page, as shown below:

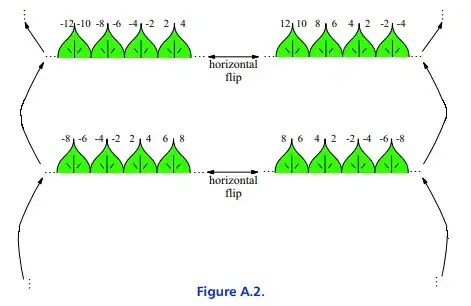
Here, the unmarked arrows represent the 'translation to right by one unit' action. For the purposes of this post however, vertical reflectional symmetry is not required, so we will instead modify the diagram to represent a quotient group of $\mathrm{p2mm}$, namely, the $\mathrm{p1m1}$ frieze group:

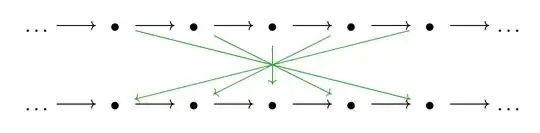
It is evident from the diagram that the axis used by the author during the horizontal flip moves during translation (the axis is always between $-2$ and $2$). Thereby this creates a group structure that appears like:

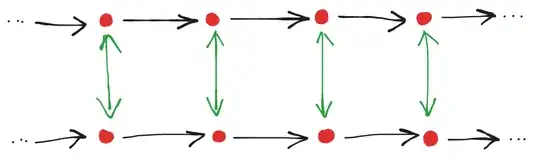
Here the green arrows represent the horizontal flip action, and the black arrows represent translation to the right by one unit (Note: the green and black arrows are not "enough" as generators, since they can't combine to create an inverse for the black action.). It is evident from the Cayley diagram that this group is isomorphic to the product group $\mathbb{Z}\times\mathbb{Z}_2$

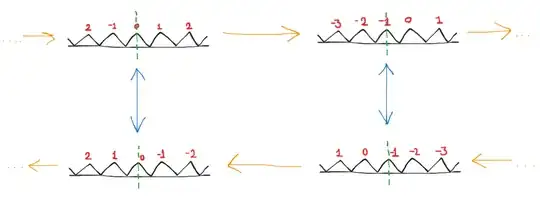
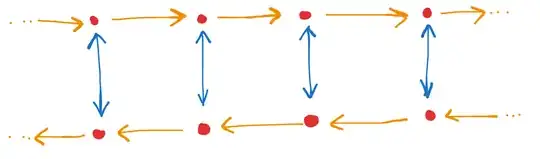
However there is another possible perspective. We could also have kept the reflection axis fixed during the translation action:

Here the yellow arrows represent the translation action and the blue arrows represent horizontal flip. Thereby, this creates a group structure which appears like:

This group appears to be isomorphic to the $\mathrm{Dih}_\infty$ group.

---

Summing up

The symmetry group of the frieze pattern $\mathrm{p2mm}$ produces the quotient frieze group $\mathrm{p1m1}$. If we use the representation of $\mathrm{p2mm}$ as shown in the book (reflection axis moves during translation), then $\mathrm{p1m1}$ is isomorphic to the abelian group $\mathbb{Z}\times\mathbb{Z}_2$. However, if the reflection axis is kept stationary over translations, then $\mathrm{p1m1}$ can instead be shown isomorphic to the non-abelian $\mathrm{Dih}_\infty$ (the infinite dihedral group).

---

Question

Based on whether the reflection axis moves during translation, we can create two different symmetry groups for the same object (the $\mathrm{p1m1}$ frieze pattern). Wikipedia tells us that $\mathrm{Dih}_\infty$ is the accepted one, which doesn’t match with the book. Why is one symmetry group preferred over another? Is it possible for an object to have two different (non-isomorphic) symmetry groups, or am I getting something wrong?

Answer 1

It is not possible for an object to have two different (that is, non-isomorphic) symmetry groups. The problem in your question is quite a subtle one: the "horizontal flip" arrows in your second picture do not all correspond to the same group element, because they are flipping relative to different axes, as you noticed. Thus, your first Cayley diagram is not accurate, as it implies that all the green arrows represent the same group element.

The symmetry group of $\mathbf{p1m1}$ is the infinite dihedral group, which is not isomorphic to the direct product $\mathbb{Z} \times \mathbb{Z}_2$, but rather to the semidirect product $\mathbb{Z} \rtimes \mathbb{Z}_2$ where $\mathbb{Z}_2$ acts on $\mathbb{Z}$ by negation.

If you were to correct the green arrows in your first Cayley diagram, it would look like this:

"Straightening" the green arrows by flipping the bottom axis yields your second Cayley diagram.