Place points on circle with constraints

Question

Context

Consider the following circle where each point on the circle is associated with a real in $[0,1)$:

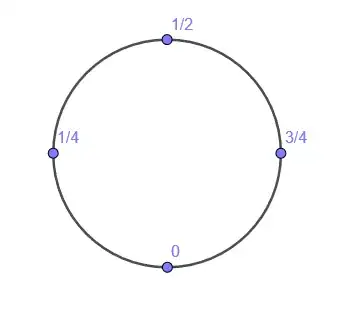
Problem

I am looking for a mathematical function $f(x)$ defined on at least $\mathbb{N}↦\mathbb{Q}+$ and range $[0,+\infty)↦[0,1)$ that can be used to place points on this circle with the following constraints (applied in order until a single point remains):

• C1: Current point must be the furthest away from any previously placed point (if any).
• C2: Current point must be the furthest away from the last placed point (if any).
• C3: Current point placement must be deterministic (no randomness).

Example

Here is a step by step example of what such a function would return ; the points on the circle will be labelled with the value of $x$.

In order to comply with C3 we arbitrary decide to apply the following logic to select a point in a deterministic way:

• C3.1: Place the initial point at $0$.
• C3.2: Consider the point on the opposite side of the circle from the last placed point, then pick the first available point moving clockwise around the circle.

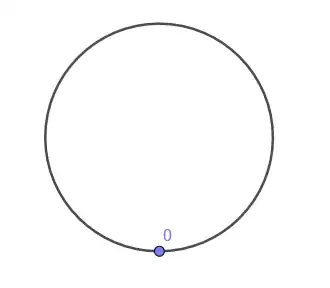
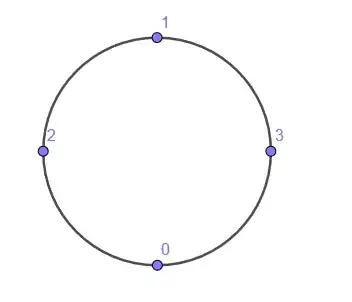
Point $0$

First point is not impacted by C1 and C2 so following C3.1 we obtain $f(0)=0$:

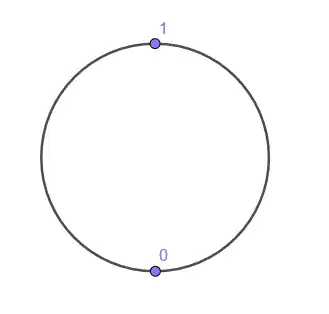
Point $1$

Apply C1 and we only have one point matching so $f(1)=\frac{1}{2}$:

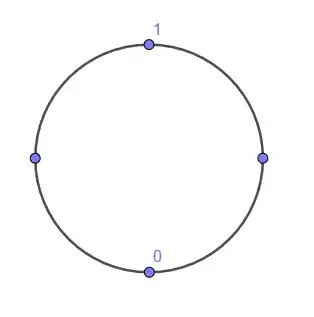
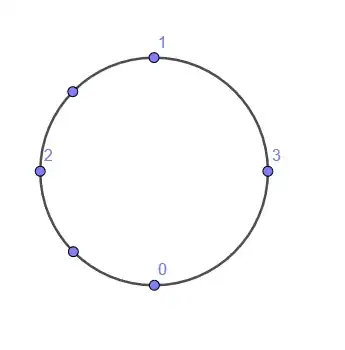
Point $2$

Applying C1 we have two possible points remaining and C2 does not allow to discriminate between them either:

Applying C3.2 selects the following point so $f(2)=\frac{1}{4}$:

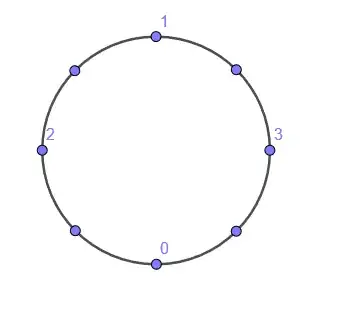
Point $3$

Applying C1 we have a single possible point so $f(3)=\frac{3}{4}$:

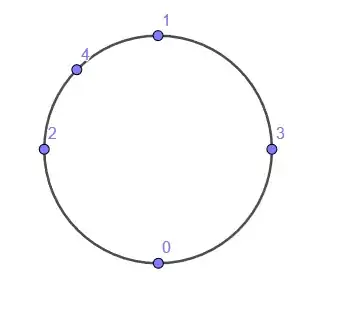
Point $4$

Applying C1 leaves us with 4 possible points:

Applying C2 leaves us with 2 possible points:

Applying C3.2 selects the following point so $f(4)=\frac{3}{8}$:

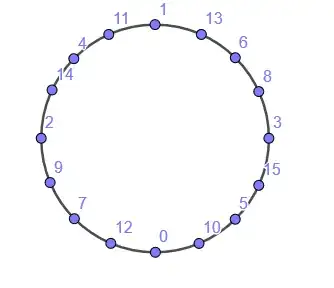
Points $5$ to $15$

Following the same logic for a few more steps we obtain:

• $f(5)=\frac{7}{8}$
• $f(6)=\frac{5}{8}$
• $f(7)=\frac{1}{8}$
• $f(8)=\frac{11}{16}$
• $f(9)=\frac{3}{16}$
• $f(10)=\frac{15}{16}$
• $f(11)=\frac{7}{16}$
• $f(12)=\frac{1}{16}$
• $f(13)=\frac{9}{16}$
• $f(14)=\frac{5}{16}$
• $f(15)=\frac{13}{16}$

Algorithmic solution

Here is an algorithm in Python that would solve the problem using the same constraints as in the example above:

def place_point(x):
    if x <= 0:
        return 0
valuesList = [0]
step = 1/2
pos = 0
# Loops from 1 to x, python range() function stops 1 unit before second param
for i in range(1, x+1):

    pos = (pos + step) % 1
    step = step/2
    tmpPos = pos
    while True:

        if tmpPos in valuesList:
            tmpPos = (pos + step) % 1
            step = step/2
        else:
            pos = tmpPos
            valuesList.append(pos)
            step = 1/2
            break

return valuesList[-1]

But as you can see this approach is not really effective due to many factors:

• It has to retain the full list of values computed (even assuming we cache the list between calls to the function, that is still ineffective).
• It does nested loops that scales with the size of that list (meaning it will run slower and slower for larger numbers).
• It relies on equality comparison between float values which is known to be unreliable in most programming languages.

Which is why I am looking for a mathematical function that would give a result in a single pass instead of this programmatic solution.

Mathematical solution

I have a quite limited mathematical background so I am clueless on where to even start in order to solve such problem, any hint in that regard would be appreciated.

The intuition that there is a mathematical solution to this problem comes from the fact that the processing is somehow cyclic, so it makes me feel like some combination of trigonometric functions should be able to give the exact solution to the problem (not only an approximation).

If you have any argument indicating that no exact solution to this problem with a single mathematical function exists, please also share them.

Any slightly different approaches to the problem that would also lead to a solution are of course welcome.

Binary approach

Following Chris Lewis' comment, here is the binary representation of the first 16 terms of the sequence above:

EDIT: Also added the binary representation of the input value in case some pattern would be visible there.

EDIT 2: After looking at the binary representations of both $x$ and $f(x)$, there is indeed some correlation between the numbers that appear: for each binary version of $x$, there is a $f(x)$ that contains the same bits but reversed. These correlated numbers seems to be grouped by "divider of power of two in $f(x)$ reduced fraction" so $f(x)=\frac{a}{2^n}$. In an attempt to organize those findings I numbered the values in each group so that we can compare their order.

$x$	$f(x)$	$x_2$	$f(x)_2$	$\frac{a}{2^n}$: $x_2$ index	$\frac{a}{2^n}$: $f(x)_2$ index
$0$	$0$	$0000_2$	$0.0000_2$	$0: 1$	$0: 1$
$1$	$\frac{1}{2}$	$0001_2$	$0.1000_2$	$2^1: 1$	$2^1: 1$
$2$	$\frac{1}{4}$	$0010_2$	$0.0100_2$	$2^2: 1$	$2^2: 1$
$3$	$\frac{3}{4}$	$0011_2$	$0.1100_2$	$2^2: 2$	$2^2: 2$
$4$	$\frac{3}{8}$	$0100_2$	$0.0110_2$	$2^3: 1$	$2^3: 3$
$5$	$\frac{7}{8}$	$0101_2$	$0.1110_2$	$2^3: 2$	$2^3: 4$
$6$	$\frac{5}{8}$	$0110_2$	$0.1010_2$	$2^3: 3$	$2^3: 2$
$7$	$\frac{1}{8}$	$0111_2$	$0.0010_2$	$2^3: 4$	$2^3: 1$
$8$	$\frac{11}{16}$	$1000_2$	$0.1011_2$	$2^4: 1$	$2^4: 6$
$9$	$\frac{3}{16}$	$1001_2$	$0.0011_2$	$2^4: 2$	$2^4: 5$
$10$	$\frac{15}{16}$	$1010_2$	$0.1111_2$	$2^4: 3$	$2^4: 8$
$11$	$\frac{7}{16}$	$1011_2$	$0.0111_2$	$2^4: 4$	$2^4: 7$
$12$	$\frac{1}{16}$	$1100_2$	$0.0001_2$	$2^4: 5$	$2^4: 1$
$13$	$\frac{9}{16}$	$1101_2$	$0.1001_2$	$2^4: 6$	$2^4: 2$
$14$	$\frac{5}{16}$	$1110_2$	$0.0101_2$	$2^4: 7$	$2^4: 3$
$15$	$\frac{13}{16}$	$1111_2$	$0.1101_2$	$2^4: 8$	$2^4: 4$

Also when C3.2 executes there is only 2 points to pick from, so we can define the conditions that always pick "the other point" as:

• C3.3: Consider the point on the opposite side of the circle from the last placed point, then pick the first available point moving counter-clockwise around the circle.

Here is the alternative sequence built by following condition C3.3 instead of C3.2 and its binary representation:

$x$	$f(x)$	$x_2$	$f(x)_2$	$\frac{a}{2^n}$: $x_2$ index	$\frac{a}{2^n}$: $f(x)_2$ index
$0$	$0$	$0000_2$	$0.0000_2$	$0: 1$	$0: 1$
$1$	$\frac{1}{2}$	$0001_2$	$0.1000_2$	$2^1: 1$	$2^1: 1$
$2$	$\frac{3}{4}$	$0010_2$	$0.1100_2$	$2^2: 1$	$2^2: 2$
$3$	$\frac{1}{4}$	$0011_2$	$0.0100_2$	$2^2: 2$	$2^2: 1$
$4$	$\frac{5}{8}$	$0100_2$	$0.1010_2$	$2^3: 1$	$2^3: 2$
$5$	$\frac{1}{8}$	$0101_2$	$0.0010_2$	$2^3: 2$	$2^3: 1$
$6$	$\frac{3}{8}$	$0110_2$	$0.0110_2$	$2^3: 3$	$2^3: 3$
$7$	$\frac{7}{8}$	$0111_2$	$0.1110_2$	$2^3: 4$	$2^3: 4$
$8$	$\frac{5}{16}$	$1000_2$	$0.0101_2$	$2^4: 1$	$2^4: 3$
$9$	$\frac{13}{16}$	$1001_2$	$0.1101_2$	$2^4: 2$	$2^4: 4$
$10$	$\frac{1}{16}$	$1010_2$	$0.0001_2$	$2^4: 3$	$2^4: 1$
$11$	$\frac{9}{16}$	$1011_2$	$0.1001_2$	$2^4: 4$	$2^4: 2$
$12$	$\frac{15}{16}$	$1100_2$	$0.1111_2$	$2^4: 5$	$2^4: 8$
$13$	$\frac{7}{16}$	$1101_2$	$0.0111_2$	$2^4: 6$	$2^4: 7$
$14$	$\frac{11}{16}$	$1110_2$	$0.1011_2$	$2^4: 7$	$2^4: 6$
$15$	$\frac{3}{16}$	$1111_2$	$0.0011_2$	$2^4: 8$	$2^4: 5$

Applications

As the question somehow ended up closed as "missing enough context", even if I believe this is still an interesting problem to solve on its own as a pure mathematical problem, here is the concrete application that motivated this question :

I was trying to get a software function that would generate a value for the hue of a HSV color for each integer you provide it, so that each color is as different as possible of the previous ones, without knowing in advance how many colors you will need.

The purpose of that function would be to automatically assign a color to a team (represented by an integer), so that you can create any number of teams on the fly and always get an automatic "unique" color for it.

Following the constraints above ensures that teams generated close to each other would always have a noticeably different color (ie: far away for each other on the hue circle).

Of course the colors generated this way starts to get pretty hard to distinguish from each other when you have a lot of them and you look at the whole list, but it does work good enough for the context where I am using it.

EDIT: Would you please elaborate what is missing for reopening this questions? I am pretty sure this answers all of the informations requested:

• background and motivation: This paragraph gives the whole background.
• relevant definitions: Is there anything in that question that is not clear enough and need more detailed definition?
• source: No extra source to quote as most of the reflection here is based on my personal work and contributions from other users.
• possible strategies: Several approaches are already listed in separate paragraphs.
• your current progress: I made several edits and update to keep the latest progress in the main post.
• why the question is interesting or important: As said at the beginning of this paragraph, this could be an interesting mathematical challenge on its own, and the current application to select a colour on the fly may also be of use in several contexts.