Formula for bump function

Question

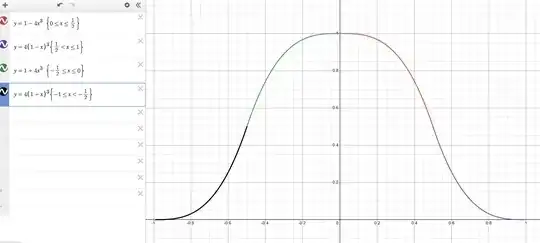
I would like to formulate a bump function (link) $f:\Bbb R \to\Bbb R$ with the following properties on the reals:

$$ f(x) = \begin{cases} 0, & \mbox{if } x \le -1 \\ 1, & \mbox{if } x = 0 \\ 0, & \mbox{if } x \ge 1 \end{cases} $$

In addition (because it's a bump function), it should be smooth and continuously differentiable, and the first-order derivative at $x = -1$ and $x = 1$ should be zero.

But one last stipulation defeats me. I would like it to be the case that

$$ \int_{-1}^1 f(x) dx = 1 $$

The example of a bump function offered in the Wikipedia article linked above comes close (I have added $1$ to the exponent to take it to a value of $1$ at $x = 0$):

$$ g(x) := \begin{cases} 0, & \mbox{if } x \le -1 \\ \exp^{1-\frac{1}{1-x^2}}, & \mbox{if } -1 < x < 1 \\ 0, & \mbox{if } x \ge 1 \end{cases} $$

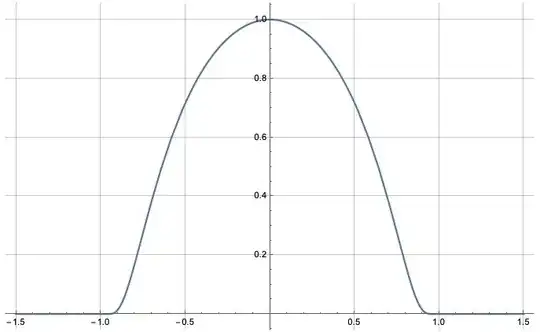
The function $g$ answers all my requirements except $\int_{-1}^1 f(x) dx = 1$. And here I hit a wall. I assume that, in principle, one could multiply $x$ by some factor $a > 1$ to obtain the precise result required... But that would require having a formula for the antiderivative $\int \exp^{1-\frac{1}{1-ax^2}} dx$, and I have no idea whatsoever how to find it. The usual techniques don't seem to apply. Furthermore, Mathematica just shrugs - which suggests to me that I could spend a very long time trying and make no progress at all.

So:

1. Is $g(x)$ in fact integrable (in the sense of producing a formula for the antiderivative)? If so, how?
2. If not, then is there a completely different formula that would satisfy the conditions set out for $f$? I really don't know how to begin constructing such a thing since my math knowledge of the properties of various classes of functions simply isn't up the task.

UPDATE AFTER SUGGESTION IN COMMENTS

I have looked at the answer here (many thanks @Lorago, I searched for "bump function" here but this didn't come up for me), but cannot make it work. Perhaps I am doing something wrong? As per the answer there, set

$$ f_0(x) := \begin{cases} 0, & \mbox{if } x \le 0 \\ e^{-\frac{1}{x^2}}, & \mbox{if } x > 0 \end{cases} $$

I can see that the function $f_1(x) := -e^{-\frac{1}{x^2}} + 1$ would produce a positive bump with $f_1(0) = 1$; though since $f_1(x) \rightarrow 0$ only as $x \rightarrow \pm \infty$, I am not sure of the utility of it. The choice of a piecewise cut-off at $x = 0$ for $f_1 (x)$ also seems odd.

However, let's go with it. The next step in the answer is to set

$$ g_0(x)=f\left(x-\frac{1}{2}\right)f\left(\frac{1}{2}-x\right) $$

So,

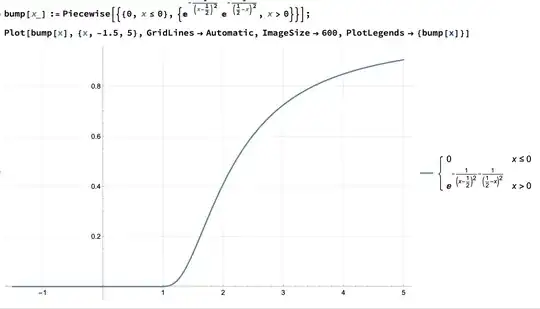
$$ g_0(x) := \begin{cases} 0, & \mbox{if } x \le 0 \\ e^{-\frac{1}{(x - \frac {1}{2})^2}} \cdot e^{-\frac{1}{(\frac {1}{2} - x)^2}}, & \mbox{if } x > 0 \end{cases} $$

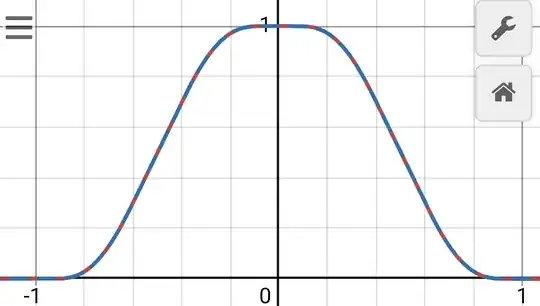
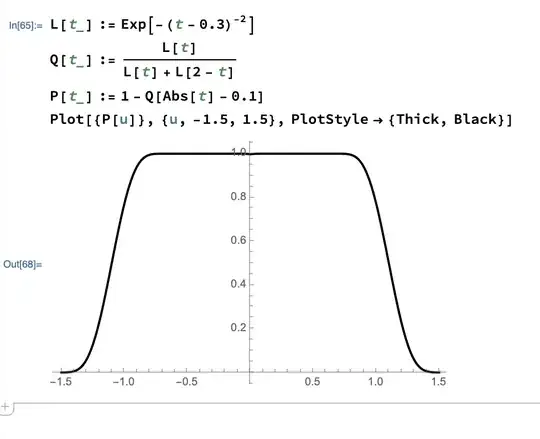
The linked answer states "This is a smooth bump function centred at the origin, but $g_0(0)\neq1$." But I beg to differ; here's a plot:

Clearly, I have deeply misunderstood what is being suggested. But for the sake of completeness, now set $g_1(x)=\frac{g_0(x)}{g_0(0)}$. Mathematica makes the following simplification:

$$ \frac {e^{-\frac{1}{(x - \frac {1}{2})^2}} \cdot e^{-\frac{1}{(\frac {1}{2} - x)^2}}}{e^{-\frac{1}{(- \frac {1}{2})^2}} \cdot e^{-\frac{1}{(\frac {1}{2})^2}}} = e^{-\frac{1}{\left(x-\frac{1}{2}\right)^2}-\frac{1}{\left(\frac{1}{2} - x\right)^2}+8} $$

So, we now have

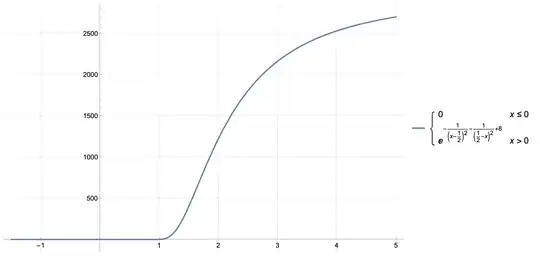
$$ g_1(x) := \begin{cases} 0, & \mbox{if } x \le 0 \\ e^{-\frac{1}{\left(x-\frac{1}{2}\right)^2}-\frac{1}{\left(\frac{1}{2} - x\right)^2}+8}, & \mbox{if } x > 0 \end{cases} $$

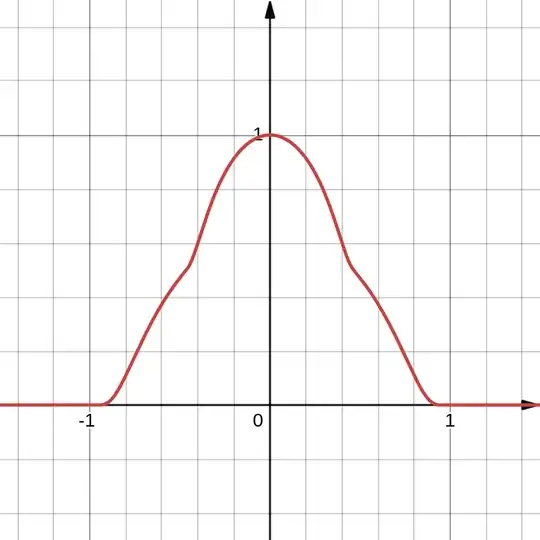
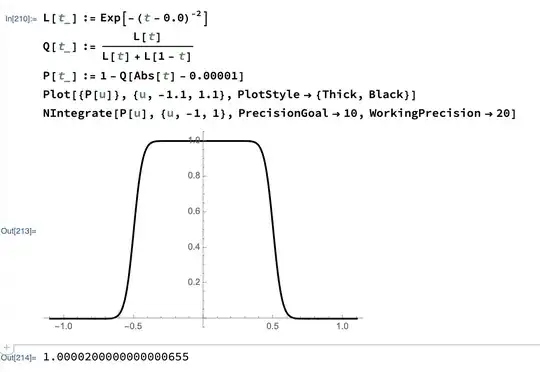
This is proposed as the solution. But it looks like this...

Even allowing for the fact that one might have made adjustments to $f_0$ to produce something more like $f_1$ with appropriate piecewise cut-offs, it's easy to see that I am doing something deeply wrong.

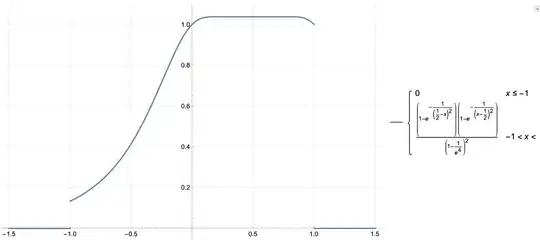
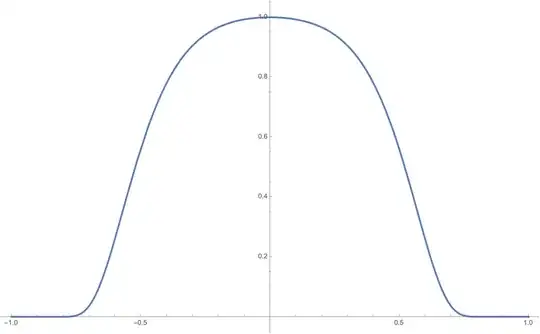
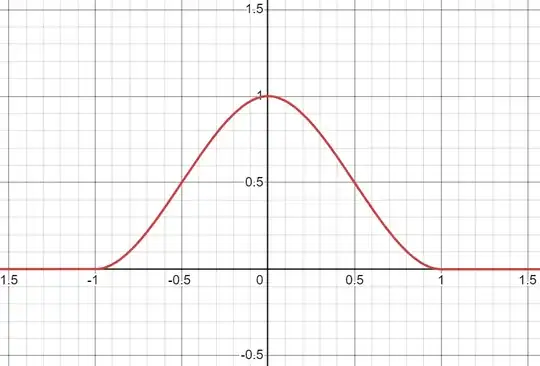
For completeness, here is a plot of the same process applied to $f_1$, with appropriate adjustments to the cut-off points for the piecewise specification. It's marginally closer but still does not address most of the requirements:

Sadly, despite the previous answer, I find myself still in need of assistance.

Answer 1

Consider the following function: $$f(x) = \begin{cases} 0,\quad x\leq -1;\\ 0,\quad x\geq 1;\\ 1,\quad x=0;\\ \dfrac{1}{1+\exp\left(\frac{1-2|x|}{x^2-|x|}\right)},\quad\text{otherwise;} \end{cases}$$

this is a smooth bump function from the family of Non-analytic smooth functions that is continuous in every point as are their derivatives, fulfills $f(-1)=f(1)=0$, $f(0)=1$, and $\int_{-1}^1 f(x)\ dx = 1$ at least in Wolfram-Alpha, so also $\int_{-\infty}^\infty f(x)\ dx = 1$, and also is a flat function at the top so have the pretty nonlinear bump function looks which is pretty similar to another example that suits your requests, the Rvachëv function $R(x)$, which is a displaced version of the first lobe of the famous Fabius function, example of an infinitely differentiable function that is nowhere analytic: you can check in this answer it fulfills your integral requirement, but it has no closed-form: in this answer a numerical approximation is shown, also it solves the Delay differential equation $R'(x) = 2R(2x+1)-2R(2x-1)$ (a good reference source for this function are the papers from Juan Arias de Reyna, year 2017).

You can check the plot of $f(x)$ in Desmos.

---

Added later

Later I realized after the comment by @10762409 that for any real valued $k$ the function: $$f(x,k) = \begin{cases} 0,\quad x\leq -1;\\ 0,\quad x\geq 1;\\ 1,\quad x=0;\\ \dfrac{1}{1+\exp\left(\frac{k(1-2|x|)}{x^2-|x|}\right)},\quad\text{otherwise;} \end{cases}$$

split the interval $[-1,\ 1]$ such as $\int\limits_{-\infty}^\infty f(x,k)\ dx = 1$, but it keeps making nice bump functions only when $k>1$, becoming a smooth approximation of the Rectangular function $\Pi(x)$ as $k\to \infty$, as could be seen in Desmos. Also, but this need to be verified, the bump function get straight-line-edges near $k\sim \frac{\sqrt{3}}{2}$. The OPs requirements are fulfilled for $k>0$.

---

Update

I was able to informally validate that the slopes of $f(x,k)$ becomes locally* straight lines at $k=\frac{\sqrt{3}}{2}$: playing in Desmos I realize that the edges going straight lines means the 2nd derivative $f_{xx}$ should get flat near these points, which happens only when $k$ is such as the 3rd derivative $f_{xxx}$ becomes zero at the point $x=1/2$, so evaluating $\frac{d^3}{dx^3}f(x,k)\Biggr|_{x=1/2}=16k(4k^2-3)=0$ which leads to $k^*=\frac{\sqrt{3}}{2}$, where the function matches at $x=1/2$ a straight line with slope $\sqrt{3}$.

(*): the function $f_x(x,\sqrt{3}/2)$ is not perfectly a flat function where it should be a straight line so is not $100\%$ accurate. In this sense, the Rvachëv function do behave accurately as straight-lines edges as you could see from the presented equation.

Desmos

---

Last Update

I was able to make a bump function with true straight-line slopes, unfortunately not in closed form but simple enough to work with it:

$$q(x)=\int\limits_{-1}^{x}u(y)dy$$

and its argument is given by the function:

$$u(x) = \begin{cases} 0,\quad |x|\geq 1\\ 0,\quad x= 0\\ 2,\quad x=-\frac12\\ -2,\quad x=\frac12\\ \dfrac{-2\,\text{sgn}(x)}{1+\exp\left(\frac{1-2||2x|-1|}{(|2x|-1)^2-||2x|-1|}\right)},\quad\text{otherwise} \end{cases}$$

I compared in Desmos $q(x)$ with an approximation of the Rvachëv function and they look really close, but they are not the same function.

Careful that since the piecewise definition of $u(x)$ I am not sure if $q(x)$ smooth $C_c^\infty$ this time (but I believe it is), but as example it clarifies why the function $f\left(x,\frac{\sqrt{3}}{2}\right)$ is not perfectly matching straight-line slopes, their derivative at the points $|x|=\frac12$ don't have flat top.

By the way, if $u(x)$ is really $C_c^\infty$, then is highly probable that $q(x)$ is also fulfilling the question requirements as a valid answer (I checked in Desmos and kind of fit numerically), but the integral $\int_{-1}^{1} q(x)dx$ should be demonstrated first (but following the comment by @10762409 it should fit).

Also, as before you could make a family of solutions $q(x,k)$ using $$u(x,k)\sim \dfrac{-2\,\text{sgn}(x)}{1+\exp\left(\frac{k(1-2||2x|-1|)}{(|2x|-1)^2-||2x|-1|}\right)}$$ which shows similar behavior than $f(x,k)$ but with true straight-line slopes.

Answer 2

I have a stricter version than what is being asked for. I have had a very similar question in the past nag at me but never figured it out. What I had been interested in was more restrictive than OP asked for. Since these types of questions about the nature of bump functions are fairly common, I have some of my thought process described at the bottom as I worked through the list of properties I wanted my solution to have.

I have a smooth bump function $f$ that has the properties:

1. $f$ is even,
2. $f\ge 0$ for all $x$,
3. $f \equiv 0$ on outside of $(-1,1)$,
4. $0 < f \le 1$ on $(-1,1)$,
5. $f(0) = 1$,
6. $f$ is decreasing away from $0$, and
7. $\displaystyle \int_{-1}^1 f(x)\,dx = 1$.

The hard part, as OP correctly identified, is making $f(0) = 1$ work with the integral being $1$. You can shrink the support of the function to obtain the desired value for the integral, but you might lose $f(0) = 1$ in the process. Or if you shrink the support and keep $f(0) = 1$, you might lose the desired value for the integral. You can add smaller bump functions supported away from $0$ after shrinking the support of the function which can work if you are careful, however your solution might not decay monotonically away from $0$.

Let $\displaystyle f_0(x) = e^{1-\frac{1}{1-x^2}}\chi_{(-1,1)}(x)$ be the standard bump function. Let $\displaystyle J = \int_{-1}^1 f_0(x)\,dx$. By this MSE post, $\displaystyle J = e^{\frac{1}{2}}\bigg(K_1\bigg(\frac{1}{2}\bigg) - K_0\bigg(\frac{1}{2}\bigg)\bigg)\approx 1.2069$, where $K_{\nu}$ is the modified Bessel function of the second kind. Define the candidate bump function $f$ by

$$f(x) = \frac{1}{1+\alpha}(f_0(2x) + \alpha f_0(x)), $$

where $\displaystyle \alpha = \frac{\frac{1}{J}-\frac{1}{2}}{1-\frac{1}{J}}$.

It is easy to see that $f$ is nonnegative and identically $0$ outside of $(-1,1)$. Since it is a convex combination of rescalings of $f_0$ and $0 \le f_0 \le 1$, we also have $0 \le f \le 1$. Likewise, $f(0) = 1$ and $f$ is decreasing away from $0$ since $f_0$ is. The tricky part is evaluating the integral of $f_0$ (which can be found in the linked MSE post), but after that, it is a simple manipulation to show that $f$ has integral $1$.

Here's a look into the thought process I had to come up with this. As for why I picked $f$ the way I did: I wanted to start with $f_0$ as it is the most common example of a bump function and OP had identified it specifically. I shrunk its support ($f_0(2x)$) to $\big(-\frac{1}{2},\frac{1}{2}\big)$ because its integral is larger than $1$. I at first added a couple of bump functions based on shifts and rescalings of $f_0$ symmetric with respect to the origin peaked near $\pm \frac{1}{2}$, but it quickly got to be difficult to manage the monotone decreasing part without getting really into the weeds. The problem was that the smaller bump functions I wanted to add had a peak and then decayed right around the edge of the support of $f_0(2x)$, so I realized that what I really wanted was a function that was flat but nonzero through the support of $f_0(2x)$, leading to using a rescaled version of $f_0(x)$. The rest was just doing a specific convex combination to make the integral and $f(0) = 1$ conditions work together.

Here is a Desmos demonstration for the function. And here is a graph demonstrating the function:

Answer 3

If you only require the first order derivative to be continuous, then you can take $$ f(x) = \begin{cases} \cos^2\frac{\pi x}{2}&\text{when $-1\leq x\leq 1$}\\ 0,&\text{otherwise} \end{cases} $$ It satisfies $f(x)=0$ when $|x|>1$, $f(0)=1,$ $f\in C^1(\mathbb R),$ and $\int f(x)\,dx=1.$

Answer 4

When you raise your function to some power $p > 0$, you can "lift" the graph up or down and change the integral this way while still having $g(0) = 1$, i.e. consider instead $$ g(x)^p = \begin{cases} \exp(p \cdot (1-\frac{1}{1-x^2})) , & \text{if } |x| < 1 \\ 0 , & \text{else} \end{cases} $$ with $p$ chosen such that $\int_{-1}^1 g(x)^p \,dx = 1$. Unfortunately, I don't think there is a closed formula to find the value of $p$ that does the trick. Solving for $p$ numerically gives me $p \approx 1.8995669372616584$.

Answer 5

I have used the $C_C^\infty$ function $$ f(x)=\left\{\begin{array}{}e^{-\frac4\pi\tan^2(\pi x/2)}\sec^2(\pi x/2)&\text{for $|x|\lt1$}\\0&\text{for $|x|\ge1$}\end{array}\right. $$ $$ \begin{align} \int_{-1}^1e^{-\frac4\pi\tan^2(\pi x/2)}\sec^2(\pi x/2)\,\mathrm{d}x &=\frac2\pi\int_{-1}^1e^{-\frac4\pi\tan^2(\pi x/2)}\,\mathrm{d}\tan(\pi x/2)\tag{1a}\\ &=\frac2\pi\int_{-\infty}^\infty e^{-\frac4\pi u^2}\,\mathrm{d}u\tag{1b}\\ &=\int_{-\infty}^\infty e^{-\pi t^2}\,\mathrm{d}t\tag{1c}\\[6pt] &=1\tag{1d} \end{align} $$ Explanation:
$\text{(1a):}$ $\frac2\pi\,\mathrm{d}\tan(\pi x/2)=\sec^2(\pi x/2)\,\mathrm{d}x$
$\text{(1b):}$ $u=\tan^2(\pi x/2)$
$\text{(1c):}$ $u=\frac\pi2t$

---

Vanishing of all derivatives at $\pmb{|x|=1}$

Note that the derivative of a polynomial in $\tan$ is another polynomial in $\tan$: $$ \begin{align} \frac{\mathrm{d}}{\mathrm{d}x}\tan^n(\pi x/2) &=n\pi/2\tan^{n-1}(\pi x/2)\sec^2(\pi x/2)\tag{2a}\\ &=n\pi/2\left(\tan^{n+1}(\pi x/2)+\tan^{n-1}(\pi x/2)\right)\tag{2b} \end{align} $$ Furthermore, $$ \begin{align} \frac{\mathrm{d}}{\mathrm{d}x}e^{-\frac4\pi\tan^2(\pi x/2)} &=-4e^{-4\tan^2(\pi x/2)}\tan(\pi x/2)\sec^2(\pi x/2)\tag{3a}\\ &=-4e^{-4\tan^2(\pi x/2)}\left(\tan^3(\pi x/2)+\tan(\pi x/2)\right)\tag{3b} \end{align} $$ Thus, by induction, for some polynomial $P_n$, $$ \begin{align} \frac{\mathrm{d}^n}{\mathrm{d}x^n}e^{-\frac4\pi\tan^2(\pi x/2)}\sec^2(\pi x/2) &=\frac{\mathrm{d}^n}{\mathrm{d}x^n}e^{-\frac4\pi\tan^2(\pi x/2)}\left(\tan^2(\pi x/2)+1\right)\\ &=e^{-\frac4\pi\tan^2(\pi x/2)}P_n(\tan(\pi x/2))\tag{4a}\\ \end{align} $$ and for any polynomial $P_n$ $$ \lim_{|x|\to1^-}e^{-\frac4\pi\tan^2(\pi x/2)}P_n(\tan(\pi x/2))=0\tag5 $$

Answer 6

Let $f(x)=\frac{\left(x^2+1\right)\text{sech}^2\left(\frac{2x}{1-x^2}\right)}{\left(1-x^2\right)^2}$ on $[-1,1]$.

This was found by constructing the anti-derivative $F(x)=\frac{1}{2}\text{tanh}\left(\frac{2x}{1-x^2}\right)$.

Answer 7

You can do this simply by stitching together four cubic curves. Start with the segment of the curve $f(x)=1-4x^3$ on the interval $[0,\frac12]$:

Rotate this curve about the point $(\frac12,\frac12)$, by adding the segment of the curve $y=4(1-x)^3$ on the interval $(\frac12,1]$:

And reflect about the $y$-axis:

This has a continuous second (but not third) derivative, and by symmetry the area under the curve is $1$.

---

Thanks to Desmos for the pictures.

Answer 8

A pretty simple one is $f(x) := (1 - x^2)^\alpha$ on $[-1, 1]$ and zero elsewhere, where $\alpha := 2.38175026...$, chosen to enforce the total integral constraint.

Answer 9

Also consider this.

I expect the code is clear enough to adapt another platforms.

Attending the comment, all we can see

Answer 10

Same technique as @TonyK's answer, but using cubic smoothstep to avoid flatness near $x=0$. Also, packaged into one equation with absolute values:

$$ \operatorname{max}\left( 0,\operatorname{sign}\left( |x|-1 \right)\left( 3x^2-2|x|^3-1 \right) \right) $$