2

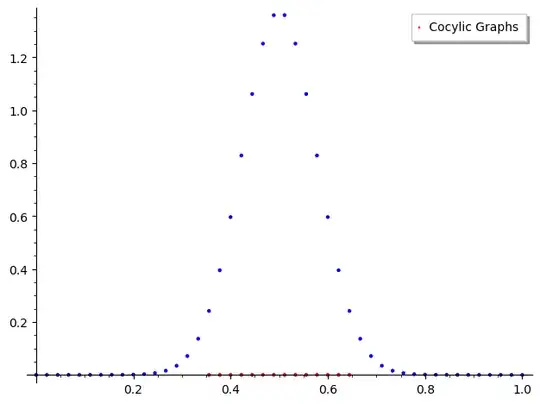
The motivation for the post comes from a pair of cocyclic graphs on 10 vertices. We call a pair of non-isomorphic graphs cocyclic if there is a bijection between the vertex sets defined by the function: $$ f(a) = b \text{ if } C_k(a) = C_k(b) $$ where $C_k$ counts the total number of closed walks of length $k$. The following is one example of a cocyclic pair (and is believed to be the smallest). 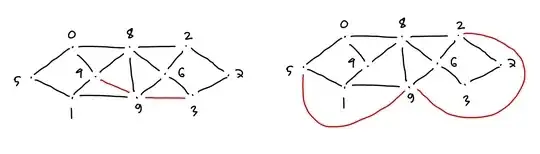Cocylic Graphs They are really rare! Only 116 exist out of 1,229,2182 graphs on 10 vertices. I haven't been able to find much literature on the construction of these graphs. I have been doing some exploring myself and I found that at least on 10 vertices, these graphs usually have a high edge count:

stats

The $y$-axis is the number of graphs and the $x$-axis: is the number of edges divided by the maximum number of edges on 10 vertices. I am trying to find works that estimate the relative frequency of such graphs as the number of vertices grows. As always, I'll be very grateful if anyone can direct me to relevant resources or even questions that are related to this.

Sajid Bin Mahamud
  • 109
  • Does $C_k(a)$ mean the number of closed walks of length $k$ starting and ending at $a$? I would have defined "cocyclic" to mean that there exists a bijection $f$ from vertices to vertices such that $C_k(a) = C_k(f(a))$. But you seem to be asking for something stronger, namely that furthermore if $C_k(a) = C_k(a')$ for all $k$ then $a = a'$? Did you intend this? If so I don't think this condition holds for the graphs you gave since it rules out the graph having a nontrivial automorphism. – Qiaochu Yuan Jul 04 '24 at 20:55
  • In any case, this condition implies but is stronger than the condition that the graphs are isospectral (https://en.wikipedia.org/wiki/Spectral_graph_theory#Cospectral_graphs) which you should be able to find literature about. – Qiaochu Yuan Jul 04 '24 at 20:57
  • Apparently the term for this condition is "cospectral vertices": https://math.stackexchange.com/questions/3741397/vertices-in-a-graph-with-the-same-number-of-closed-walks – Qiaochu Yuan Jul 04 '24 at 21:09

0 Answers0