Integrating both sides differential equations

Question

$$5\frac{dx}{dt}=(20-x)(40-x)$$

I understand, that we can treat derivatives as fractions, and arrive at the correct solution. So rearranging,

$$\frac{5}{(20-x)(40-x)}dx=dt$$ However, now I get confused. I know we can integrate both sides, but when we integrate, we need to integrate with respect to something else. Here the solution just places an integral sign in front of both, hence the right side integrates with respect to $t$ and the other with respect to $x$. So why can we just place two integrals, without integrating with respect to something else.

To me, integrating makes no sense if we are not integrating with respect to some variable.

Edit: For example, even when we implicitly differentiate, we take the derivative of all the terms with respect to some variable, in some sense this is the reverse process, but what are we integrating with respect to? I understand the $dx$ and $dt$ are already there, but don't we have to integrate with respect to a common variable on both sides first?

Answer 1

What is usually done with separation of variables is abuse of notation. Formally it can be justified with integration of both sides with respect to $t$ $$ f(x) \cdot x' = g(t)$$ $$ \int f(x) \cdot x' dt = \int g(t) dt$$ Now we can use substitution in the integral on left hand side $$ \int f(x) \cdot x' dt = \left| \begin{matrix} x = x(t) \\ dx = x'dt \end{matrix} \right|= \int f(x) dx $$ Using this identity in the original integration we get the same result as with the abuse of notation $$ \int f(x) dx = \int g(t) dt $$

Answer 2

$\mathbf {dx}$ is a so called differential form, that is a locally linear function on local vectors $\mathbf v$ along curves of points $\mathbf P= \mathbf x = (x,y) \in \mathbb R ^2$, defined by

$$\mathbf{dx}\left (\ v_x(x,y)\ e_x(x,y) \ + \ v_y(x,y) \ e_y(x,y)\ \right) \ = \ v_x(x,y).$$

$\mathbf {dx},\mathbf {dy}$ may be defined by their action on the gradient field of a function

$$\mathbf dx((\partial_x f(x,y),\partial_y f(x,y))=\partial_x f(x,y)$$

especially on the linear coordinate function themselves

$$\mathbf {dx}(\partial_x x)=1, \mathbf {dx}(\partial_y x)=0 $$

and their inverses as integrals along curves

$$\int_{C= (a x +b,d y + e)} \mathbf {dx} = \int_{C= ( \xi +b,d y + e)} \frac{ \mathbf {d\xi}}{a}$$

A differential of first order is an equation between those linear functions

$$ \omega (\mathbf v (\mathbf x))= \sum_i a_i(\mathbf x )\ \mathbf {dx}_i(\mathbf v (\mathbf x)) = 0$$

Such an equation makes sense by the trivialities of linear algebra: the linear functions to the number field form a linear vector space, too, called the dual space. So the linear combinations of differential forms are a differential form. In other words, if points on parallel lines define vectors, families of parallel hyperplanes define the linear space of 1-forms.

The zero of such a differential form eavluated on vectors defines a vector field, that is a local field of directions in n-dimensional space.

The differential equation for sine function

$$y'=\sqrt{1-y^2}, \quad \omega = \mathbf {dy} - \sqrt{1-y^2} \mathbf {dx} =0 $$ yields the following vector field

\[Omega][x_,y_]:= Line[{{x,y}, {x,y}+0.1 (  #/Norm[#]&)[{1,Sqrt[1-(y)^2]}]}]
Graphics[{{Opacity[0.4], Red, 
    Table[[Omega][x, y], {x, -[Pi]/2, [Pi]/2, [Pi]/20}, {y, -1, 1, 1/30}]}, 
    {Plot[Sin[x], {x, -[Pi]/2, [Pi]/2}][[1]]}}, 
     Frame -> True, FrameTicks -> {{-[Pi]/2, 0, [Pi]/2}, {-1, 0, 1}} ]

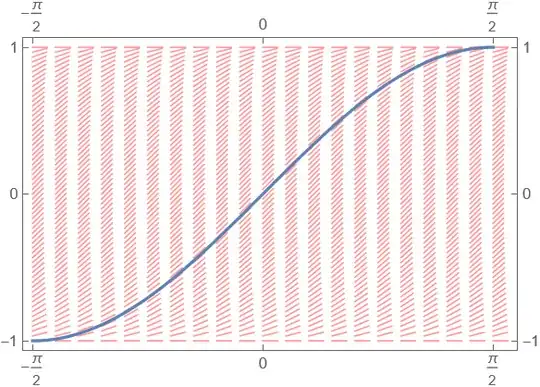
To solve a differential equation of first order means to find in a family of differentiable curves $\mathit C_{\mathbf x_0}$ fitting such a 2d vector fields and passing throug a given point $\mathbf x_0$

$$s\to \mathbf x\left( s, \ \mathbf x_0\right),$$

such that the action of the differential form onto its tangent at all points yields zero.

Only in two dimensions there is the simple identity

$$f\left(y',(x,y)\right) \ = \ 0 \ \leftrightarrow y' = f^{-1}(x,y) \leftrightarrow \mathbf{dy}= f^{-1}(x,y) \ \mathbf {dx}$$

As you see in the image, beware of points $(x,y=\pm 1$ where the inversion of the coefficient functions isn't working.

If $ f(y',(x,y)) =0 $ is linear in $y'$ one has a simple linear form. Only of the coeffients separate, the differential form is exact, $$y'= f(y) g(x) \ \leftrightarrow \ \frac{dy}{f(y)} - dx \ g(x)=0$$ and their integrals can be done directly and differ by a constant.

In general, a differential form is not the differential of a function, but it's possible to find an integrating factor $\mu(xy)$, such that there exists a solution function $g$

$$\mathbf {dx} \ \partial_x g(x,y) + \mathbf {dy} \ \partial_y g(x,y) = \mu(x,y) \left(\mathbf {dx} \ - f(x,y) \mathbf {dx} \right) ==0$$

Its typical, that solutions of an ordinary differential equation are presented by the zero of a family of functions of several variables.

Often the inverses are defined as series of a 'special function' with the same name as the defining equation.

This scheme is universal for systems of explicit ODE's of any order: they can always be reduced to linear systems of first order by renaming all derivatives as independent variables, exceptfor the two highest derivatives in

$$y^{(n)}(x) = F\left(y^{(n-1)}(x),\dots y(x)\right)$$ $$y^{(n)}\to z_{n-1}'(x),\quad y^{(k)}(x)\to z_k(x) $$