Sangaku problem: Show that five circles have equal radii.

Question

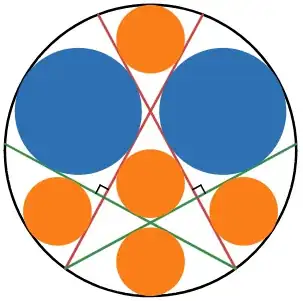
Inspired by Sangaku problems such as these, I created the following Sangaku problem.

---

Consider the following diagram.

Description: The diagram shows the circle $x^2+y^2=1$, two red chords with equations $y=\pm mx+k$ where $m>1$ and $0<k<1$, and two green chords that each meet one of the red chords on the circle below $y=0$ and is perpendicular to the other red chord. The values $m$ and $k$ are chosen so that there exist two blue circles inside the unit circle that are reflections in the $y$-axis, the left of which is tangent to: the unit circle, the chord $y=mx+k$ at the midpoint of the chord $y=mx+k$, the chord $y=-mx+k$, and the chord perpendicular to $y=mx+k$.

Inscribe five orange circles as shown below. (The orange circles are inscribed in every previously unoccupied region except the two triangles.)

Show that the five orange circles have equal radii.

I have a computer-assisted solution. I am looking for a computer-free solution.

---

My computer-assisted solution

Define the following four points:

• $(x_1,y_1)$: Point where the right blue circle touches the chord $y=-mx+k$.
• $(x_2,y_2)$: Point where the right blue circle touches the unit circle
• $(x_3,y_3)$: Centre of the right blue circle
• $(x_4,y_4)$: Lower-left point where the chord $y=mx+k$ meets the unit circle

$x_1$ is the average of the sum of roots of $x^2+(-mx+k)^2=1$, so $x_1=\frac{mk}{1+m^2}$ and $y_1=\frac{-m^2k}{1+m^2}+k$.

$x_2$ is the larger root of $x^2+\left(\frac{x}{m}\right)^2=1$, so $x_2=\frac{m}{\sqrt{1+m^2}}$ and $y_2=\frac{1}{\sqrt{1+m^2}}$.

$x_3=\frac12(x_1+x_2)=\frac12\left(\frac{mk+m\sqrt{1+m^2}}{1+m^2}\right)$ and $y_3=\frac12\left(\frac{k+\sqrt{1+m^2}}{1+m^2}\right)$.

The distance from $(x_3,y_3)$ to the chord $y=mx+k$ equals the radius of the right blue circle, which is $R=\frac12\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$. This gives one equation with $m$ and $k$.

$x_4$ is the smaller root of $x^2+(mx+k)^2=1$, so $x_4=\frac{-mk-\sqrt{1+m^2-k^2}}{1+m^2}$ and $y_4=\frac{-m^2k-m\sqrt{1+m^2-k^2}}{1+m^2}+k$. The centre of the right blue circle, $(x_3,y_3)$, lies on the line that passes through $(x_4,y_4)$ with gradient $1$. This gives another equation with $m$ and $k$.

With help from Wolfram, I solved these two equations to get an approximation of $m$, then put this approximation back into Wolfram, which suggested it is the real root of a certain cubic polynomial. Using this method, I got:

• $3m^3-6m^2+3m-4=0\implies m\approx1.8491482$
• $17k^3-33k^2+30k-6=0\implies k\approx0.2681854$
• $17R^3-54R^2+57R-16=0\implies R\approx0.4362138$ ($R=$ radius of blue circles)

Let $S$ be the radius of the orange circle nearest the centre of the unit circle. It is easy to show that $\frac{R}{S}=m$ (note that the obtuse angle between the green chords equals the obtuse angle between the red chords, then compare the central orange circle and a blue circle). Again with the help of Wolfram, this gives:

• $17S^3-30S^2+57S-12=0\implies S\approx 0.2358999$

Assuming that the five orange circles have equal radii, I used the closed forms for $m,k,R,S$ to make a desmos graph of the diagram, and all the circles and chords fit together perfectly.

---

Fun fact: The centres of the top four circles are the vertices of a square.

This comes from the fact that the distance from the centre of the top orange circle to the intersection of the red chords, which is $1-S-k$, equals $x_3$.

(Other Sangaku problems that I created are here and here.)

Answer 1

Here's a partial result in the form of a dynamic sangaku that generalizes some elements of this puzzle and @heropup's solution to one of OP's previous offerings.

If a circle lies tangent to a bounding circle and the midpoint of a chord thereof, then tangents to that circle from any point on the "other" arc of the bounding circle determine a trio of congruent inscribed circles as shown.

My proof of this is currently a bit messy, but expressing the endpoints of the chord, and the point on the arc, in terms of their angular offsets from, say, the "north" point of the bounding circle seems to give reasonably nice trigonometric forms to relevant lengths.

For instance, if the bounding circle has unit radius, the angular offset to a chord endpoint is $2\theta$, and the offset to the arbitrary point on the arc is $2\phi$, then the radii of the big circle and smaller circles are, respectively, $$\sin^2\theta \qquad\text{and}\qquad \sin^2\theta\left(1-\frac{\sin^2\theta}{\sin^2\phi}\right)$$

Anyway, with this result in hand, only the lower-most one of OP's circles remains to be considered.

---

Addendum. A GeoGebra sketch strongly suggests that at least some aspects the construction continue indefinitely:

(It seems I have my own variant of OP's seashell motif. :)

Drawing additional tangents from the chosen point to the pair of "outermost" circles sitting above the chord gives two more congruent circles tangent to the bounding circle; the associated circles inscribed in triangles under the chord are also congruent to each other, albeit not to new above-chord circles.

It'll take some work to determine if there's any nice pattern in the radii ... and/or if there's any "obvious" reason all three of those first-step circles (marked with dots in the figure) are congruent.

---

Addendum 2. (It seems as though I may never get around to answering the question itself!)

In trying to streamline my analysis of these inscribed circles, I stumbled onto a surprising(-to-me) connection with the notion of power of a point.

Consider points $A$, $B$, $C$, $D$ arranged around $\bigcirc O$ (of radius $r$), making successive central angles $$\angle AOB=4\theta_0 \quad \angle BOC=4\theta_1 \quad \angle COD = \angle 4\theta_2 \quad \angle DOA = 4\theta_3$$ where $\sum \theta_i = 90^\circ$. Lines $AC$ and $BD$ determine four circles tangent to $\bigcirc O$; let $\bigcirc U_i$ (with radius $u_i$) correspond to $\theta_i$.

Consider separately points $A'$, $B'$, $C'$, $D'$, and their antipodes $A''$, $B''$, $C''$, $D''$, arranged around a separate copy of $\bigcirc O$, making successive central angles $$\angle A'OB'=2\theta_0 \quad \angle B'OC' =2\theta_1 \quad \angle C'OD' = 2\theta_2 \quad \angle D'OA''=2\theta_3 \quad \cdots$$ for the same $\theta_i$ as before. The sides of inscribed rectangles determined by $A'C'$ and $B'D'$ meet at points $V_0$, $V_1$, $V_2$, $V_3$ (and their reflections in $O$), with $V_i$ (of distance $v_i$ from the center) in the sector corresponding to $\theta_i$.

The two separate configurations are related quite concisely:

$$r u_i \;=\; - \operatorname{pow} V_i \tag{$\star$}$$

More verbosely, $$r u_i \;=\; \frac{4r^2}{\left(\,\cot\theta_i-\tan\theta_{i+2}\,\right)\left(\,\cot\theta_{i+1}+\cot\theta_{i+3}\,\right)} \;=\; r^2-v_i^2 \;=\; -\operatorname{pow}V_i \tag{$\star'$}$$ with index arithmetic performed modulo $4$, of course.

With appropriate adjustments, these relations apply when the $\bigcirc U_i$ are externally tangent to $\bigcirc O$. I'll leave the reader to ponder on this. I've already typed too much (and I'm not done yet!).

I imagine that a relation as elegant as $(\star)$ must have been discovered long ago, but I haven't done a literature search.

Be that as it may ...

---

Using $(\star)$, I can prove two-thirds of the theorem at the top of this answer; namely, that the two smaller above-the-chord circles are congruent.

Consider $\triangle ABC$ and its circumcircle (with center $O$ and radius $r$). Let $\bigcirc U$ (with radius $u$) be tangent to the circle and to $AB$ at its midpoint, let chords $CP$ and $CQ$ be tangent to $\bigcirc U$.

Dilate $A$, $B$, $P$, $Q$ in $C$ onto $A'$, $B'$, $P'$, $Q'$ on the circle with radius $r$ about $C$. Let $C'C''$ be the diameter of $\bigcirc C$ tangent to the circumcircle.

By the Inscribed Angle Theorem, we know that angles at $C$ formed by $A'$, $B'$, $P'$, $C''$ are halves of corresponding central angles formed by $A$, $B$, $P$, $C$ at $O$. Focusing on $\bigcirc U$ being determined by $AB$ and $CP$, we deduce that chords $A'B'$ and $C''P'$ meet at point $V$ (at distance $v$ from $C$), satisfying $(\star)$; thus, $$r u = r^2- v^2$$ (Likewise, as $\bigcirc U$ is determined by $AB$ and $CQ$, chords $A'B'$ and $C'Q'$ meet at $V$.)

Now, we "know" $|AB|=2r\sin C$ in $\triangle ABC$; with $\bigcirc U$ tangent to $AB$ at its midpoint, we readily calculate $u=r\sin^2\frac12C$. Thus, $v=r\cos\frac12C$, which implies that $V$ is the midpoint of $A'B'$ in isosceles $\triangle A'B'C$.

Knowing this, it follows that chords $P'C'$ and $Q'C''$ meet $A'B'$ at points $V_P$ and $V_Q$ equidistant from $V$. (This is the Butterfly Theorem.)

$V_P$ and $V_Q$ are necessarily equidistant from $C$, and thus also are equally-powered relative to $\bigcirc C$. Since they are the "rectangle points" corresponding to centers $U_P$ and $U_Q$ of other inscribed circles determined by $AB$ and $CP$ and $CQ$, relation $(\star)$ guarantees that these circle have the same radius. Hence, the proposition is two-thirds proven, as claimed. (The final third —that the circle inscribed in $AB$, $CP$, $CQ$ is congruent to the other two— is left as an exercise to the reader.) $\square$

Is this the easiest demonstration that $\bigcirc U_P$ and $\bigcirc U_Q$ are congruent? Maybe not, but I'm actually rather pleased with it. And I think the connection to the Butterfly Theorem is pretty neat.

(Hmmm ... The result uses a butterfly inscribed in a semicircle. I wonder if there's an inscribed-circle sangaku that corresponds to a general butterfly in an analogous way.)

NOW I'm done typing.