Counting ones in binary representation: When is the product multiplicative?

Question

Question:

For $n \in \mathbb{Z}^+$, define $Z(n)$ to be the number of ones in the binary expression of $n$. For fixed positive integer $a$, how does one describe the set of $b$ such that $Z(ab) = Z(a)Z(b)$?

---

---

Bounty Added (Jun 6, 2024):

So far there is one answer provided, and I received a similar answer by email that I paste below; additional ideas and reference pointers are most welcome!

Edit (Jun 4, 2024): In response to two different comments: Corrected an image and introducing Hamming weight, which (in the case of binary strings) refers to the total number of ones in a string. With this additional vocabulary item, the main question can be rephrased as asking when the Hamming weight is multiplicative.

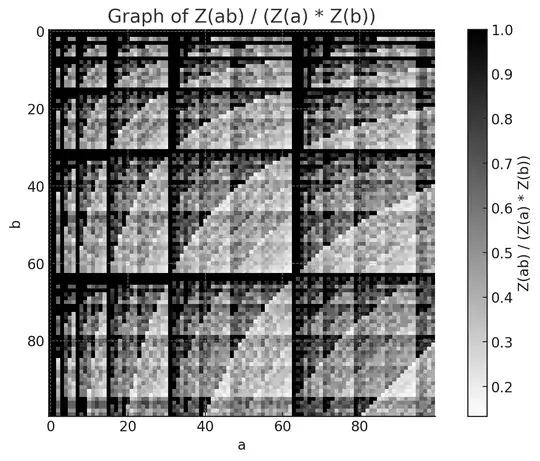
Edit (Jun 3, 2024): I used GPT-4 (link) to create graphs with the following query:

consider a positive integer n. define Z(n) to be the number of ones in the binary representation of n. create a 100 by 100 graph where (a,b) is colored black if Z(ab)=Z(a)*Z(b), and colored white otherwise.

Here is an image of the graph that was produced:

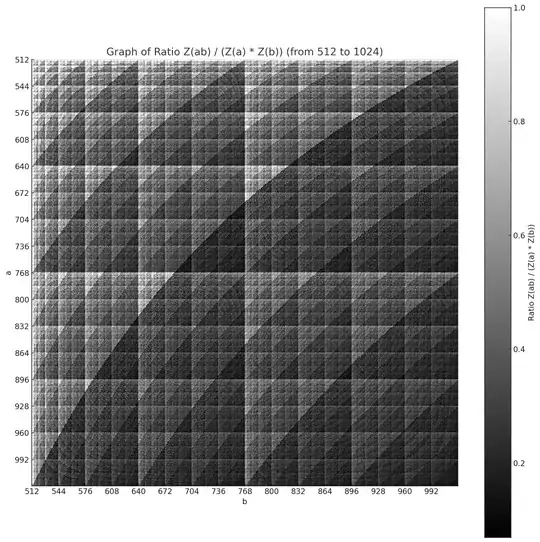
Because of a pattern that looks like the Sierpinski Triangle in the bottom right hand corner of this graph, I followed up by specifically printing graphs where both $a,b$ are in the range $[64, 128]$ and then $[128,256]$. Those images are pasted below:

I suspect this Sierpinski pattern holds for $a,b$ in $[2^k, 2^{k+1}]$ for large $k$, but am not sure how to prove it. Ideas in this direction are welcome, although the intention of this initial question is the bolded question of the top.

---

Edit asked by author (Jun 8, 2024):

Beautiful $100\times100$ plot (generated by GPT-4o) of the ratio $Z(ab)/(Z(a)Z(b))$ as shades of gray, as dvitek proved that this ratio was in $[0, 1]$.

Answer 1

Here is another definition of $Z(a)$: $Z(a)$ is the minimum number of distinct powers of two needed to write $a$ as a sum of powers of two. (The minimal representation is unique up to the order of the summands.)

Let $a = 2^{a_1} + 2^{a_2} + \cdots + 2^{a_{Z(a)}}$ and $b = 2^{b_1}+2^{b_2} + \cdots + 2^{b_{Z(b)}}$ be two minimal representations. Now $$ab = \sum_{i, j} 2^{a_i+b_j}.$$ So clearly $Z(ab) \le Z(a)Z(b)$, with equality iff none of the $a_i+b_j$ coincide (for then we can combine the colliding summands into a larger power of two). If $a_i + b_j = a_k + b_l$ (for $i \neq k$ and $j \neq l$), then $a_i - a_k = b_j - b_l$. Hence $Z(ab) = Z(a)Z(b)$ precisely when the difference sets of $A = \{a_1, \cdots, a_{Z(a)}\}$ and $B = \{b_1, \cdots, b_{Z(b)}\}$ are disjoint.

This explains several patterns seen in your graphs. For example, if $a = 2^k$, the difference set of $\{k\}$ is empty so there is no restriction on $b$. Similarly, there are more possible $b$s when the binary representation of $a$ is sparse, because then the difference set of $A$ is small (hence easier to avoid). And the Sierpinski-like patterns arise due to numbers having the same difference sets.

Answer 2

I've created a Python code that draws the grayscale plot of the function $Z(ab)/(Z(a)Z(b))$ (see below). Sizes of powers of $2$ generates self-similar fractal that gets more detailed as the power of $2$ gets larger. Perhaps the most beautiful picture is at size $512$ (as they do also get more grayish).

It's interesting to note there are grid-like and quasi-circular patterns. The distorsion in the circular arcs reminds me of the function $|x|^n + |y|^n = 1$.

Feel free to use the code to experiment (or just get nice pictures)!

import numpy as np
import matplotlib.pyplot as plt

def compute_Z_values(size):
    """Compute Z values for all numbers from 1 to size using dynamic programming."""
    Z_values = [0] * (size + 1)
    for i in range(1, size + 1):
        Z_values[i] = Z_values[i >> 1] + (i & 1)
    return Z_values

size = 2**9

# Compute Z(a) for all a in [1, size**2] using dynamic programming
Z = compute_Z_values(size**2)

# Initialize the grid
grid = np.zeros((size, size))

# Fill the grid
for a in range(1, size + 1):
    for b in range(1, size + 1):
        grid[a-1, b-1] = Z[a*b]/(Z[a]*Z[b])

# Create the plot
plt.imshow(grid, cmap='gray', origin='upper')
plt.colorbar(label='Ratio Z(ab) / (Z(a) Z(b))')
plt.title('Gray scale representation of Z(ab) / (Z(a) Z(b))')
plt.xlabel('a')
plt.ylabel('b')
# Save the plot
plt.savefig('Z_plot_' + str(size) + '.png
# Show the plot
plt.show()

Note that changing gray to gray_r in plt.imshow, swaps the blackness and the whiteness.

---

Edit: Gray scale representation for $a, b \in [2^9, 2^{10}]$: