Prof gave us wrong definition of convexity?

Question

My professor gave us this exercise:

---

Let $f : \mathbb{R} \rightarrow \mathbb{R}$ be a differentiable function. Given the following two definitions of convexity of $f$, prove that (i) implies (ii):

(i) $\forall x, y \in \mathbb{R} : f(x) \ge f(y) + f'(y)(x - y)$

(ii) $\forall x, y \in \mathbb{R}, \forall \lambda \in [0, 1] : f(\lambda x + (1 - \lambda)y) \le \lambda f(x) + (1 - \lambda)f(y)$

---

I think definition (i) is incorrect. I think it would be correct, if we would assume $x,y$ arbitrary but we must have $x \geq y$. Since (i) is differently written:

$$\frac{f(x)-f(y)}{x-y} \ge f'(y)$$

So the gradient/slope from $y$ to $x$ is greater than the slope of $y$. That makes sense because in a convex function the slope increases.

But if we choose $y$ to be greater than $x$, then it's wrong.

Let me give this example:

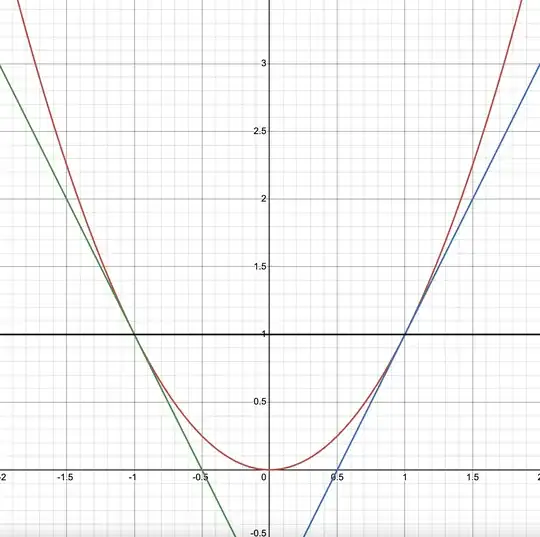
We have $f(x)=x^2$ and $x,y=\pm 1$. The slope from $x$ to $y$ (or $y$ to $x$) is $0$. It's the black line in the plot. The slope at $-1$ is $-2$, that's the green line. So we indeed have $-2 \le 0$. But if we pick $x$ and $y$ to be $x=-1$ and $y=1$, then the statement (i) is false, since it would state that $0 \ge 2$.

So to me it seems, the correct definition would be:

(i) $\forall x, y \in \mathbb{R}$ with $x \ge y : f(x) \ge f(y) + f'(y)(x - y)$

Answer 1

$f(x) \ge f(y) + f'(y)(x - y)$ is only equivalent to $\frac{f(x)-f(y)}{x-y} \ge f'(y)$ when $x - y > 0$. In order to rewrite the first inequality into the second one, you have to divide by $x - y$, and when $x - y < 0$, this reverses the direction of the inequality.

Indeed, for your example, if you check the original inequality, you have $f(x) = 1$, $f(y) = 1$ and $f'(y) = 2$, so $f(y) + f'(y)(x - y) = 1 + 2(-1 - 1) = 1 - 4 = -3$, which is less than $f(x) = 1$.

And more generally, if $f(x) = x^2$, then $f(y) + f'(y)(x - y) = y^2 + 2y(x - y)$. By completing the square (with respect to $y$), this can be rewritten as $x^2 - (x - y)^2$. Since $(x - y)^2$ is always greater than or equal to zero, this expression is always less than or equal to $f(x) = x^2$.

The intuition you should have for (i) is that it states that the function always lies entirely above its tangent lines. $T(x) = f(y) + f'(y)(x - y)$ is the point-slope form of the equation of the line tangent to $f$ at $y$.

Answer 2

I think you have to be careful when rewriting that inequality. Notice that the equality would be different if x-y was negative when dividing. Try your values in the original inequality, given.