Analyzing Cumulative Distribution Functions in Sampling Without Replacement vs. With Replacement

Question

I am studying a population of $N$ bits, comprising $K$ ones and $N-K$ zeros. For sampling $n$ bits without replacement, the situation conforms to a hypergeometric distribution. The sum of these $n$ bits, $S_n$, yields a mean of $n\frac{K}{N}$ and a variance of $n \frac{K}{N} \frac{N-K}{N} \frac{N-n}{N-1}$. Conversely, sampling $n'$ bits with replacement aligns with a binomial distribution, with the sum $S_{n'}$ having a mean of $n'\frac{K}{N}$ and a variance of $n' \frac{K}{N} \frac{N-K}{N}$.

For my analysis, I plotted the cumulative distribution functions (CDFs) for the normalized sums $\frac{S_n}{n}$ and $\frac{S_{n'}}{n'}$, considering values of $n'$ within the range $\left[n,\lfloor n\frac{N-1}{N-n}\rfloor\right]$. I observed that for normalized sums exceeding $\frac{K}{N}$, the binomial CDF consistently lies below the hypergeometric CDF. The trend is longer followed for $n'>n\frac{N-1}{N-n}$. It is noted that the variance of the normalised hypergeometric distribution is lower than that of the binomial distribution if $n'<n\frac{N-1}{N-n}$.

If $X$ is a hypergeometric distribution with n draws without replacement from a population of size $N$ with $K$ successes and $Y$ is a binomial distribution $B(n',K/N)$, then what is the maximum $n'$ for which $F_Y(f n')\leq F_X(f n)$ for $f\geq K/N$?.

I suppose that the maximum $n'= \lfloor n\frac{N-1}{N-n}\rfloor$.

Heres an animation for $\frac{K}{N}=0.5$, with $N=50$ where the number of binomial trials is fixed at $n'=n\frac{N-1}{N-n}=21$ and number of hypergeometric trials is fixed at $n=15$. The portion marked green is the region where the normalized sums are greater than $p=\frac{K}{N}$. In this region the binomial CDF is below the hypergeometric CDF.

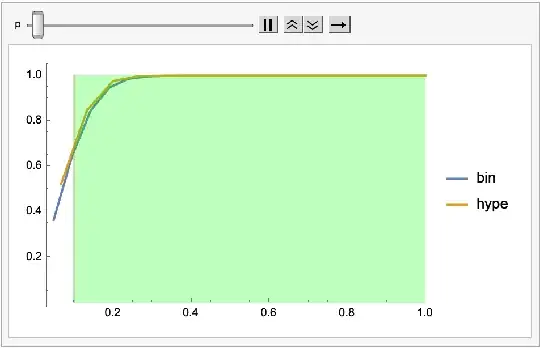
I'm curious if this relationship between the distributions' CDFs is a recognized phenomenon. Does anyone know of relevant research articles on this topic?

Additionally, here’s the Mathematica code used for generating these plots, adjustable for different $p=K/N$ values:

Manipulate[Nx = 10^2;
 n = 30;
 x = p Nx;
 ListPlot[{Table[{k/Floor[binomialtrials], 
     CDF[BinomialDistribution[Floor[binomialtrials], p], k]}, {k, 1, 
     Floor[binomialtrials]}], 
   Table[{k/n, 
     CDF[HypergeometricDistribution[n, Floor[x], Nx], k]}, {k, 1, 
     n}]}, Joined -> True, PlotRange -> All, 
  PlotLegends -> {"bin", "hype"}, 
  Epilog -> {RGBColor[0, 1, 0, 0.25], Rectangle[{p, 0}, {1, 1}], Red, 
    Line[{{p, 0}, {p, 1}}]}], {binomialtrials, n, n (Nx - 1)/(Nx - n),
   1}, {p, 10^-2, 1}]

Does anyone have insights or references which might explain this pattern?

EDIT

Let $h(x;n,N,K)$ denote the probability mass function of the hypergeometric distribution and $b(x;n,p)$ that of binomial distribution, where $p=K/N$.I need to compare the hypergeometric distribution and the modified binomial distribution, where the number of samples $n'=a n$, where $a= \frac {N-1}{N-n}$.Denoting $x'=a x $, let us first figure out the ration $\frac{h(x;n,N,K)}{b(x';n',p)}$. Note that in general $x'$ and $n'$ need not be integers. For simplicity lets start by assuming they are. Now we can compare the probabilities.

$$ \begin{aligned} \frac{h(x;n,N,K)}{b(ax;an,p)}&=&\frac{b(x;n,p)}{b(ax;an,p)}\frac{h(x;n,N,K)}{b(x;n,p)}\\ &=&\frac{{n\choose x}p^x(1-p)^{n-x}}{{an\choose ax}p^{ax}(1-p)^{a(n-x)}}\frac{h(x;n,N,K)}{b(x;n,p)}\\ &=& \frac{n!}{x!(n-x)!}\frac{(ax)! (a(n-x))!}{(an)!}p^{x-ax}(1-p)^{(n-x)-(a(n-x))}\frac{h(x;n,N,K)}{b(x;n,p)}\\ \end{aligned} $$ Applying stirlings approximation $n!\sim \sqrt{2 \pi n}\left(\frac{n}{e}\right)^n$, we get,

$$ \begin{aligned} \frac{h(x;n,N,K)}{b(ax;an,p)}&\sim&\sqrt{a}\left(\frac{(1-x/n)^{n-x}(x/n)^{x}}{(1-K/N)^{n-x}(K/N)^{x}}\right)^{a-1} \frac{h(x;n,N,K)}{b(x;n,p)}\\ &\sim& \sqrt{a}\left(\left(\frac{N}{n}\right)^n\left(\frac{x}{K}\right)^x\left(\frac{n-x}{N-K}\right)^{n-x}\right)^{a-1}\frac{h(x;n,N,K)}{b(x;n,p)}\\ \end{aligned} $$

I'm stuck here. My goal here is to proceed similar to this answer by LPZ.

Answer 1

You can more easily prove this in the limit $N\to\infty$. Indeed, if $K = pN+o(N)$, then the hypergeometric distribution of parameters $N,K,n$ converges to the binomial distribution of parameters $p,n$. You can calculate the next to leading order terms to compare the two. To better estimate the next to leading effect, I'll assume $K = pN+o(1)$. The crossing of the cdf's at $K/N$ is normal since both take the value $1/2$ at the mode.

For actual calculations, it is easier to focus on the pmf. Your behaviour can be explained by the fact that the hypergeometric distribution is more concentrated at its mean than the limiting binomial distribution. Quantitatively: $$ \begin{align} P(X=k) &= \frac{\binom Kk\binom{N-K}{n-k}}{\binom Nn} \\ &=\binom nkp^n(1-p)^{n-k}\frac{\prod_{i=1}^{k-1}\big(1-\frac i{pN}+o(1/N)\big)\prod_{i=1}^{n-k-1}\big(1-\frac i{(1-p)N}+o(1/N)\big)}{\prod_{i=1}^{n-1}(1-i/N+o(1/N))}\\ &= \binom nkp^n(1-p)^{n-k}\left(1+\frac{(n-1)n-\frac{(k-1)k}p-\frac{(n-k-1)(n-k)}{1-p}}{2N}+o(N^{-1})\right) \end{align} $$ You can check that the next to leading order correction is negative for $k\in(k_-,k_+)$ and positive in the complement. $k_\pm$ are the real roots of: $$ (n-1)n=\frac{(k-1)k}p-\frac{(n-k-1)(n-k)}{1-p} $$ This gives you the observed concentration effect. Furthermore, due to the overall $1/N$ factor, the behaviour is asymptotically monotone, i.e. the if $N>N'$ then the pmf for $N$ lies between the pmf for $N'$ and the pmf for the binomial distribution.

Technically, the previous analysis does not apply to your case, since you have at best $K = pN+O(1)$ when taking the closest integer. This means that the next to leading order term is drowned in the resulting $O(1/N)$ error term. However, the formula still holds since the $O(1)$ error is rigorously bounded by $1$. Therefore, for $k$ far from the roots $k_\pm$ (i.e. where the quadratic function takes values outside $(-1,1)$), it will give the correct sign of the discrepancy, so you can still conclude which curve is over the other.

Hope this helps.