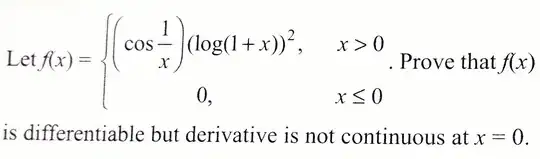Actually I'm arriving to a different result and seems that the question might be wrong I've mentioned what I've tried please help me figure out my mistake any help is appreciated,thanks in advance!

Asked
Active
Viewed 67 times
-2
Anonymous
- 537
-
1Please type the content in the image: If the entirety of the answer remains as an image, this post will likely be downvoted and closed. – J.D Apr 20 '24 at 21:00
-
3That is not how you prove a function is differentiable. – qqo Apr 20 '24 at 21:01
-
2Use the limit definition of the derivative to prove $f$ is differentiable at $x=0$. The derivative itself is not continuous at $x=0$. – Clayton Apr 20 '24 at 21:02
-
This kind of question is a mega-duplicate. See for instance https://math.stackexchange.com/questions/689529 – Anne Bauval Apr 21 '24 at 10:31
1 Answers
0
You used the behavior of $f$ when $x > 0$ to decide if $f$ is differentiable at the origin, so really what you are showing is that $$ \text{lim}_{x \to 0+} f'(x) $$ does not exist. But it's possible that $f'(0)$ exists, and this would just mean that $f'$ is not continuous at the origin.
What if you use the definition of the derivative instead, which works out to
$$ \lim_{h \to 0} \frac{f(h)}{h}? $$
Clearly that limit is $0$ from the left. From the right, you have $$ \lim_{h \to 0} \frac{1}{h} \cos\big(\frac{1}{h})(\log(1+h))^2. $$ This limit exists and is $0$ (the log term has order of vanishing $2$, which takes care of the $1/h$ and still has enough left to deal with the annoying oscillating cosine).
hunter
- 32,629