The probability of a circle in a circumscriptible polygon

Question

I have difficulty understanding the solution below and have already summarized my difficulties as follows,

1. why "the area of the polygon $abcelef$ .... represents the number of ways the three points can be taken, so that the circle circumscribing the triangle will lie wholly within the given polygon." It looks like the ratio of the two areas is the probability that a circle with a given radius lying wholly in the polygon.
2. "An element of the polygon at $G$ is $4 x d x d \psi$", what does the "element" mean? a differential form? and why is it $4 x d x d \psi$;
3. why is an element of the polygon at $R$ $dt$?
4. why is $dt$ only a differential form of $d\theta$? why not include $dx$ too?
5. why do we introduce an imaginary angle $\phi$?

Problem:

A circle is circumscribed about a triangle formed by joining three points taken at random in the surface of a circumscriptible polygon of $n$ sides, find the chance that the circle lies wholly within the polygon.

Solution:

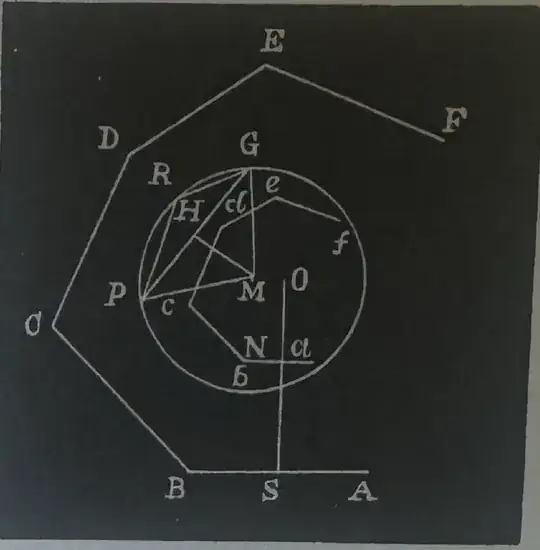
Let $ABCDEF\ldots$ be the polygon, $PGR$ the triangle formed by joining the three random points $P$, $G$ and $R$, $O$ the center of the entirely circumscribing $PGR$ (which I think is a typo, should be $M$ rather than $O$). Draw the polygon $abcef$..., making its sides parallel to those of the given polygon, and at a distance from them equal to $MP$, and draw $ONS$ and $MH$ perpendicular to $AB$ and $PG$. Check the figure below

Now while $PG$ is given in length and direction, and $\angle PRG$ is given, if $MP$ is less than the radius of the inscribed circle of the given polygon, the area of the polygon $abcelef\ldots$ represents the number of ways the three points can be taken, so that the circle circumscribing the triangle will lie wholly within the given polygon.

Let $PG =2x$, $OS =r$, perimeter of $ABCDEF\ldots$ $=s$, area of segment $PRG$ $=t$, area of sector $PMG$ $=v$, area of triangle $PMG$ $=u$, area of polygon $ABCDEF\ldots$ $= \Delta$, $\angle PMH = \theta$, $\phi=\sin ^{-1}(\frac{x}{r})$, and $\psi=$ the angle which $PG$ makes with some fixed line.

Then we have $PM = x \csc \theta$, $ON = r - x \csc \theta$, area $abcdef \ldots$ $=(r - x \csc \theta)^{2} \frac{\Delta}{r^{2}}$, $v = \theta x^{2} \csc^{2} \theta$, $u = x^{2} \cot \theta$, $t=v-u$, and $dt = dv - du = 2 x^{2} \csc^{2} \theta(1 - \theta \cot \theta) d \theta$.

An element of the polygon at $G$ is $4 x d x d \psi$, or $4 r^{2} \sin \phi \cos \phi d \phi d \psi$, and at $R$ it is $dt$. The limits of $x$ are $0$ and $r$; of $\phi$, $0$ and $\frac{1}{2} \pi$; of $\theta, \phi$ and $\pi - \phi$; and of $\psi$, $0$ and $2 \pi$.

Hence, doubling, since $R$ may lie on either side of $PG$, wo have for the required chance,

\begin{align*} p &=\frac{2}{\Delta^3} \int_0^r 4 x d x \int_{\theta=\phi}^{\theta=\pi-\phi} d t \int_0^{2 \pi} d \psi(r-x \csc \theta)^2 \frac{\Delta}{r^2}\\ &=\frac{16 \pi}{r^{2}\Delta^2} \int_0^r x d x \int_{\theta=\phi}^{\theta=\pi-\phi} d t(r-x \csc \theta)^2\\ &= \frac{32 \pi}{r^2 \Delta^2} \int_0^r x^3 d x \int_\phi^{\pi-\phi}(r - x \csc\theta)^{2}(1 - \theta \cot \theta) \csc^2 \theta d\theta\\ &= \frac{2 \pi r^{4}}{3 \Delta^2} \int_0^{\frac{1}{2}\pi} [2(\pi-2 \phi) \sin 2 \phi+4-4 \cos 4 \phi-3 \sin ^2 2 \phi \cos 2 \phi+64 \sin^{4} \phi \cos \phi \log \tan \frac{1}{2} \phi] d \phi\\ &= \frac{2 \pi^2 r^{4}}{5 \Delta^2}\\ &=\frac{8 \pi^2 r^2}{5 s^2} \\ \end{align*}

Remarks

If $ABCDEF \ldots$ is a circle, $s = 2\pi r$, so $p = 2/5$, and the problem is from the book "Inside Interesting Integrals" written by Prof. Paul J, Nahin, which is stated as follows,

Imagine a circle (let’s call it $C_{1}$) that has radius $a$. We then chose at random (i.e., uniformly distributed) and independently, three points from the interior of that circle. These three points, if non-collinear, uniquely determine another circle, $C_{2}$. $C_{2}$ may or may not be totally contained within $C_{1}$. What is the probability that $C_{2}$ lies totally inside $C_{1}$? See the answer

Answer 1

Below I am trying to make the asked points clear, computations do not stay in focus. First of all a picture:

The problem starts somehow with the middle, making the least number of words in a random language count for exposing the problem. This is not the way we think, and not the way we start solving. Instead, let us introduce the objects in their order.

• The circle $\mathcal O$ with center $O$ in the origin and radius one is given. (The general case is translated and rescaled to this one.)
• A polygon $\Pi=ABCDEF\dots$ circumscribed to $\mathcal O$ is chosen. So $AB$, $BC$, $CD$, $DE$, $EF$, $\dots$ are all tangent to $\mathcal O$.
• The parameter $r$ is the distance from $O$ to the side $AB$, so $r=1$, i must have as few variables to look at as possible.
• The situation so far is fixed.
• Consider the probability space $\Omega$ of three points $(P,R,G)$ inside $\Pi$, seen as a "solid area", the (closed) convex hull of its vertices. Denote such a triple always by $(P,R,G)$ with $P,R,G\in\Pi^3$. A measurable subset $Z\subset \Pi^3$ is an event of $\Omega$, it has the tacitly chosen probability $$ \Bbb P(E) =\frac 1{\operatorname{Area}(\Pi)^3}\int_Z 1\; dP\; dR\; dG =\frac 1{\Delta^3}\int_Z 1\; dP\; dR\; dG\ . $$
• We can construct now functions depending on $P,R,G$. For instance, $M=M(P,R,G)$, the circumcenter of $\Delta PRG$ is such a function with values in $\Bbb R^2$. And the projection $H=H(P,R,G)$ is an other function $H:\Omega\to\Omega\subset \Bbb R^2$. Both are continuous, thus measurable. Also, $x=x(P,R,G)=\frac 12|PG|$, half the length of the side $PG$ is such a function. (It does not depend on $P$.)
• And all the other letters that are involved in the quick solution are also (continuous, thus measurable) functions on $(P,R,G)$. For instance the circumradius function $(P,Q,R)\to \rho(P,R,G):=|MP|=|MR|=|MG|$. One should once for all times make an alphabet with a clear order and same letters in all languages, this simplfies typing. Here $M$ is the function $M=M(P,R,G)$ already introduces. Lengths of segments are now without the pipe symbols.
• Draw now parallels at distance $\rho=\rho(P,R,G)$ from the sides of $\Pi$ taken on the same side as $O$, and $\Pi$. Intersect the parallels to obtain a polygon $\Xi=\Xi(P,R,G)=abcdef\dots$ with sides parallel to those of $\Pi=ABCDEF\dots$. They are similar, so the quotient of the areas is the square of the proportionality factor. Here $a,b,c,d,e,f,\dots$ are also seen as functions of $(P,R,G)$.
• Introduce now the random variables (where random does not refer to the way letters and their order were chosen) $x,s,t,v,u,\Delta,\theta,\phi,\psi$.
• We want to compute the integral using a change of variables. So in few moments the above letters are variables. We only write dependencies between variables.
• $(P,R,G)$ is our starting parameter, we integrate w.r.t. $dP\; dR\; dG$, so we have an integral in $\Bbb R^6$, six parameters / degrees of freedom of integration are needed. If we use the cartesian notations $P=(x_P,y_P)$, $R=(x_R,y_R)$, $G=(x_G,y_G)$, then the measure under the normed integral is explicitly $$ dP\; dR\;dG = dx_P\; dy_P\; dx_R\; dy_R\; dx_G\; dy_G \ . $$ From these six given parameters $(P,R,G)$ we manufacture other.
• Consider the map $(P,R,G)\to(P,R,(x,\psi))$. Here $2x$ is the length of $PG$, and $\psi$ the angle it makes with some fixed line, e.g. with the $Ox$ axis. It corresponds to a change to polar variables in $G$, $$ (x_P,y_P,x_R,y_R,x,\psi) (x_P,y_P,x_R,y_R, \underbrace{x_P+2x\cos \psi}_{x_G}, \underbrace{y_P+2x\sin \psi}_{y_G})\ . $$ Here the domain of definition of the new parameter is what it is, $(x_P,y_P,x_R,y_R)\in\Bbb D^2$, but the last two parameters depend on $(x_R,y_R)$. The domain will suffer further transformations, till we get it under control. The transformed volume element is formally $$ \begin{aligned} & dx_P\; dy_P\; dx_R\; dy_R\; dx_G\; dy_G \\ &\qquad = dx_P\wedge dy_P\wedge dx_R\wedge dy_R\wedge dx_G\wedge dy_G \\ &\qquad= dx_P\wedge dy_P\wedge dx_R\wedge dy_R\wedge d(x_P+2x\cos \psi)\wedge d(y_P+2x\sin \psi) \\ &\qquad= dx_P\wedge dy_P\wedge dx_R\wedge dy_R\wedge d(2x\cos \psi)\wedge d(2x\sin \psi) \\ &\qquad= 4\; dx_P\wedge dy_P\wedge dx_R\wedge dy_R \wedge (\cos \psi\; dx-x\sin\psi \; d\psi) \wedge (\sin \psi\; dx+x\cos\psi \; d\psi) \\ &\qquad= 4x\; dx_P\wedge dy_P\wedge dx_R\wedge dy_R \wedge dx \wedge d\psi \\ &\qquad=4x\; dx_P\; dy_P\; dx_R\; dy_R\; dx\; d\psi \end{aligned} $$ (or use Jacobian determinants in absolute value for the transformation if the wedges are unclear), so we formally replace $dG=4x\; dx\; d\psi$. This is the story at the point with the "volume element of the polygon around $G$".
• When I continue in this manner there is no soon end of the story, so I will say what will be replaced by what new variables.
• We replace $x$ by $\phi$, so that formally $\phi=\arcsin x$, $x=\sin \phi$, $dx=d(\sin\phi)=\cos\phi\; d\phi$, so the part in $x$ in the last volume element, that $4x\; dx$ gets replaced by $4\sin\phi\;\cos \phi\; d\phi$. Our new parameter is $(P,R,\phi,\psi)$
• From $(P,R,\phi,\psi)$ we can quickly recover $G$, and then build $M$ and $\Xi=abcdef\dots$, so consider $M,\Xi$ as functions of the new parametrization. However, from $M,\phi,\psi$ we can recover $R$, so we pass to the new parameter $(M,R,\phi,\psi)$, and formally $dR=dM$, since $R,M$ are obtained from each other by a (variable) translation involving the other variables. Our new parameter comes with the volume element: $$ 4\sin\phi\;\cos \phi\; dM\;dR\;d\phi\;\psi \ , $$
• It is time to control the range for some parameters. The main observation, and the reason for the geometric constructions, is that the circumcircle $\odot(PRG)$ is completely contained in $\Pi$, iff $M$ is in $\Xi=abcdef\dots$ - because so $M$ has distance at least $MP$ to all the sides. Then we perform integration first w.r.t. $dM$, and we have an expression for the area of $\Xi$ , the proportionality $(ON:OS)^2$ is needed, now recall $OS=r=1$, and $ON=OS-NS=1-MP$.
• We have to do now something with the parameter $R$. For this, i will make a quick passage to the following choice of parameters, and their order is important.
  • We make a choice of $x\in[0,1]$. Recall that the radius of $\mathcal O$ is $r=1$. This constrains in the picture the length $2x$ of the segment $PG$, wherever its final destination and determination in terms of the following parameters will be. We have $PH=HG=x$. We may use $\phi=\phi(x)=\arcsin x$ as a function of $x$ in the resulted integral.
  • The directions of $PHG$ and $MH$ determine each other, this is the parameter $\psi$. So far we have a fixed segment $PG$ with mid point $H$ to move on the plane parallel to a fixed direction.
  • Let us now fix the parameter $\theta=\widehat {PMH}$. Together with $x$ it completely determines the measures of $\Delta MPH$, which we now model in wood and search for one of its good places inside $\Pi$. In particular the radius $MP$ of the final $\Delta PRG$ is now nailed down. We use it to get the point $N$ on $OS$ with $NS=MP$. Construct $\Xi$ similar to $\Pi$, so that the boundary of $\Xi$ is at distance $MP$ in the exterior to the boundary of $\Pi$.
  • Fixing $\theta$ is done in the same time with restricting and parametrizing $R$. It lives in the one or the other sector of bounded by $MP$ and $MG$, and the triangle $\Delta MPG$ is removed. This parametrization is not the one I would make, details are then hidden in the computations.
  • Now it is time to fix the vertex $M$ of our wooden triangle $\Delta MPG$ inside $\Xi$. Then $M,P,G$ are fixed, and $G$ also finds its final place. How many parameters are burned so far? Five, one for each $x,\psi,\theta$, and two for $M$.

---

To the questions:

1. The area of the polygon $\Xi = abcdef\dots$ represents strictly speaking the integral over $\Xi=\Xi(x,\theta)$ w.r.t. $dM$, so it takes from the initial integral w.r.t. $dP\; dR\; dG$ a part $dM$, where $dM$ is replacing inside of a parametrization the $dP$. This is all only "lyrics", but the steps above show some details.

2. The "volume" or rather "area element" is $dG$, and after the parametrization of $G$ as $P+2x(\cos \psi,\sin\psi)$ we have $dP\wedge dG=dP\wedge 4x\; dx\; d\psi$. So in the presence of $dP$ (and $dR$) the change of variables from $G$ to $(x,\psi)$ feels like passing to polar coordinates. We formally replace $dG$ from the whole integral.

3. It is again a matter of reparametrizing $R$ in terms of $\theta,t$ with the meanings defined by the text. Then $dR$ is expressed in a specific manner in terms of $d\theta\; dt$ (times a Jacobian factor).

4. Including $dx$ would not change things, since we compute something like $dx\wedge dR$, and $dx\wedge ?$-two-forms obtained after rephrasing $dR$ are cancelled. Or put it in another way. We apply Fubini, and split the set of good cases $Z$ w.r.t. $x$, so for each $x$ we have a set $Z_x$ to further integrate the remained parameters.

5. The angle $\phi$ controls the range for $\theta$, so that the resulted $PM$, radius of the circle $\odot(M)=\odot(PRG)$ does not exceed one. It is used only as a function of $x$ in a tacit manner, making $\theta$ run only between $\phi$ and $\pi\phi$, i.e. $PM=\frac x{\sin\theta}=\frac {\sin\phi }{\sin\theta}\le 1$.