8

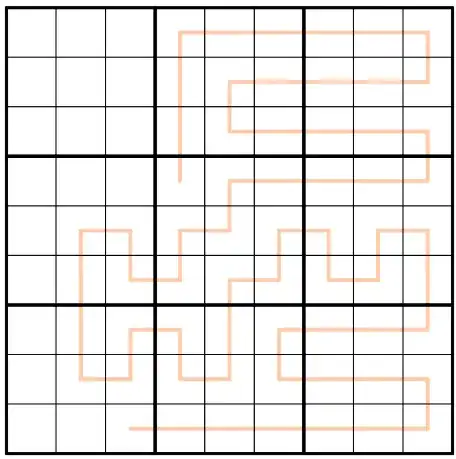
I stumbled upon a problem which seems easy but is actually hard to answer. It involves the sudoku game and a commonly used custom constraint rule called "entropic lines".

The rules of a normal 9x9 sudoku puzzle are: Each row and column and 3x3 box contain the digits 1-9 once each. The rules for entropic lines are: Any set of three sequential cells along an entropic line must contain a low digit (1,2,3), middle digit (4,5,6) and high digit (7,8,9).

The question I am trying to answer is:

Does a valid sudoku solution exist for a grid with one entropic line covering all 81 cells which does not overlap itself and only move horizontally and vertically?

I tried bruteforcing it for a few hours with no solution. Here is an example of grid with a long line I found, that also has a solution (more than one): example

Jam
  • 10,632
  • 3
  • 29
  • 45
Aura Lee
  • 263
  • 1
    Interested to see your grid with the line covering 79 cells. – DreiCleaner Mar 12 '24 at 18:04
  • 1
    @DreiCleaner I edited the post. – Aura Lee Mar 12 '24 at 18:13
  • 1
    One possible strategy: fix a desired entropic path in advance, and then seeing whether there's a valid Sudoku with that entropic path is an integer linear programming problem. – Greg Martin Mar 12 '24 at 18:40
  • If you get rid of the block rule for Sudoku, can you come up with a solution? If not, another possible strategy (for showing nonexistence): fix the path, then show that there exists some row or some column such that there aren't 3 of each kind. It might be easier than working with the block rule. – Varun Vejalla Mar 12 '24 at 20:02

1 Answers1

8

No.

Focus on the green squares:

checkerboard

It is known that every digit must appear in the green cells an even number of times. This is a consequence of set equivalence theory.

WLOG the line starts with a low digit (1-3), then medium (4-6), then high (7-9), and repeats this order.

Since there are 40 green squares, and 41 white squares, the line must start and end on white squares, and visit green squares on every other step.

Therefore the first green square contains a medium digit, the second contains a low digit, the third contains a high digit, and the cycle repeats.

This means that there are 14 medium digits, 13 low digits, and 13 high digits in the green squares. Since 13 is an odd number, there must be some digit occurring an odd number of times in the green cells, which contradicts the earlier statement.

Kendall Frey
  • 646