Integral via Contour Integration involving many-valued functions

Question

In E.G.Phillips Functions of a complex variable it is stated that for an integral of the form $\int_{0}^{\infty}x^{a-1}Q(x)dx$ where $a \in \mathbb{R}$ is not necessarily an integer, the contour to be used is the following (the wavy line indicates a cut on the complex plane for $\Re(z)>0$):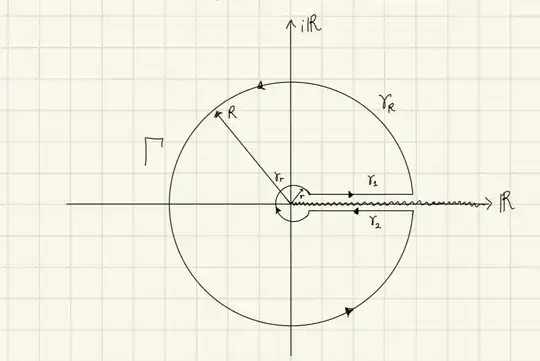

Then it goes on to say that we must pay attention to the point on the upper and lower edge of the cut since the complex number(written in polar form $z = \rho e^{i\theta}$) acquires a phase. For example, if I have defined $\theta = \theta_p + 2\pi n, n \in \mathbb{Z}$, then $\theta_p = 0$ when we approach the cut from above, whereas $\theta_p = 2\pi$ when we approach the cut from below. I understand the problem given by the plane cut (for more details, I usually refer to the following answer https://math.stackexchange.com/a/3512489/1096913), anyways I don't get how I should implement this fact when parametrizing $\gamma_1, \gamma_2$. In particular, I'd like to see how to use this particular contour with a basic example (always regarding the segments that lie just above and below the cut, since I know how to compute the integration along the other ones). Thanks in advance.

Answer 1

There is a very nice example in Conway's Functions of One Complex Variable I, 2nd edition, Springer, pages 119-120, which is worked out in much detail over two pages. It uses $Q(x)=\frac{1}{1+x}$ and $a \in ]0,1[$ but the method is actually quite general. For obvious copyright reasons I cannot reproduce the full example, but for what you particularly request, here is how the gist of the solution goes.

The main technical issue is that to evaluate the integral you must consider a branch of the function $z^{-c}$ (I posit $c = 1-a$ to follow Conway's example more easily).

Let $G = \{z: z \neq 0 \land 0 < \arg z < 2\pi \}$. You have to define a branch $l$ of the logarithm function on G by putting $l(r e^{i\theta} ) = \log(r) + i\,\theta,$ where $0 < \theta < 2\pi$. For $z$ in G, you now posit $f(z) = e^{- c\,l(z)},$ so that $f$ is a branch of $z^{-c}$. Considering now the notations of your curve and adapting Conway's example accordingly, $\Gamma=\gamma_1+\gamma_R+\gamma_2+\gamma_r$.

The evaluation of the posted integral is based on the Residue theorem applied to the countour integral with the same integrand and $\Gamma$ as a contour, let us call $I$ the result of this computation. You then go on proving that

$$\int_r^R x^{-c} Q(x) dx = \lim_{\delta\to 0^+} \int_{\gamma_1}f(z)Q(z)dz \tag{1},$$

where $z=x+i\delta \in \gamma_1, x\in \mathbb{R}$. Similarly, using the fact that $l(\overline{z})=\overline{l(z)}+2\pi i$

$$-e^{-2\pi\,i\,c}\; \int_r^R x^{-c} Q(x) dx = \lim_{\delta\to 0^+} \int_{\gamma_2}f(z)Q(z)dz \tag{2},$$ where $z=x+i\delta \in \gamma_2, x\in \mathbb{R}$. You now have to let $r\to0$ and $R\to\infty$ with adequate assumptions on $Q$ in such a way that the parts of the contour integral corresponding to $\gamma_r$ and $\gamma_R$ vanish in the limit.

You can now equate the result of the computation of integral $I$ with the sum of $(1)$ and $(2)$ with bounds at the limits, from which equation you can derive the value of $\int_0^\infty x^{-c} Q(x) dx$ by some simple algebra.