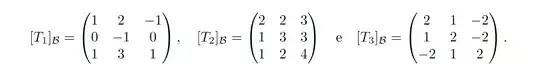This question is from an older exam of Linear Algebra of my university, it's one of 14 questions of the exam. They want to know which of these matrices are diagonalizable. The problem is: I can't see any way of doing it quickly (<10minutes). The first is OK, but the second and the third one is a real problem if you need to calculate the eigenvalues and eigenvectors of them. There are also no diagonal matrices. Can someone help?
A nice trick my professor taught me was to see if you can eyeball any eigenvectors right from the start. The reason why this is helpful is if we make a change of coordinates using a basis that contains at least one eigenvector, then we can work with a simpler matrix, as at least one of the columns will consist of two or more zeros. Let's use the second matrix in the example you sent. One thing I noticed is that the entries in each row add up to $7$, so if we multiply the matrix by the vector $(1,1,1)$ (i.e., add all the columns together), we get the vector $(7,7,7)$, so we have an eigenvector with eigenvalue $7$! Let $\mathcal{B}'$ be the basis $\mathcal{B}'=\{(1,0,0), (0,1,0), (1,1,1)\}$. If you work out the matrix $[T_2]_{\mathcal{B}'}$, which won't take long due to the nice basis, you'll get a lower triangular matrix, and finding the determinant of this amounts to multiplying the diagonals, so you can very quickly find that the characteristic polynomial is given by $c_{T_2}(x)=(x-1)^2(x-7)$. From here, you just need to check that $\dim(E_1)=2$, and you're done. This might not be the fastest method, but it will definitely decrease the amount of computations.
For the first two matrices, there are quick tricks that are applicable to $3 \times 3$ matrices (and for the first more generally) by which we can come to the conclusion that the matrices is diagonal.
For the first matrix $A = [T_1]_{\mathcal B}$, the key is to notice that the matrix has a row/column consisting of zeros except on the diagonal. In particular, the second row has zeros except for the $-1$ on the diagonal. By expanding $\det(A - \lambda I)$ with a Laplace expansion along the second row, we find that
$$
\det (A - \lambda I) = -0 \det\pmatrix{?&?\\?&?} + (-1 - \lambda) \det \pmatrix{1 - \lambda & -1\\1 & 1 - \lambda} - 0 \det \pmatrix{?&?\\?&?}\\
= (-1 - \lambda)\pmatrix{1 - \lambda & -1\\1 & 1 - \lambda}.
$$
So, our characteristic polynomial is $(-1-\lambda)$ multiplied by the characteristic polynomial of the $2 \times 2$ matrix $\pmatrix{1 & -1\\1 & 1}$, which means that the eigenvalues of $A$ are $-1$ together with the eigenvalues of this smaller matrix. If we recognize this $2 \times 2$ matrix as a matrix of the form $\pmatrix{a & -b\\b & a}$, then we can quickly ascertain that its eigenvalues are $a \pm bi$, which is to say $1 \pm i$. Thus, $A$ has distinct eigenvalues $-1, 1-i, 1+i$. So, $A$ is diagonalizable.
The second matrix $B = [T_2]_{\mathcal B}$ can be written as a rank-1 matrix added to a multiple of the identity. That is, we can write $B = uv^T + tI$ for some column-vectors $u,v$ and scalar $t$. Such a matrix is diagonalizable if and only if $uv^T$ is diagonalizable.
To check whether $B$ is of this form, we could begin by "blanking out" the diagonal entries. Consider the matrix $$ \pmatrix{?&2&3\\ 1&?&3\\ 1&2&?}. $$ Is there a way that I can fill in the blanks in order to make this matrix rank-1? Yes: writing in the entries $1,2,3$ means that I have the same row repeated $3$ times. Can we get these entries by replacing $B$ with $B + tI$? Yes: the rank-1 matrix we described is $B - I$.
So, $B$ has the same eigenvectors as the rank-1 matrix $$ B - I = \pmatrix{1&2&3\\ 1&2&3\\ 1&2&3}, $$ so it suffices to determine whether $B-I$ is diagonalizable. $B-I$ has an eigenvalue of $0$ with multiplicity $2$, the question is simply whether $B$ has a non-zero eigenvalue (which would necessarily have a one-dimensional associated eigenspace). In order to check whether this is the case, calculate the trace of $B - I$, which is the sum of its eigenvalues. We calculate $$ \operatorname{tr}(B - I) = 1 + 2 + 3 = 6. $$ So, $B-I$ has an eigenvalue of $6$. So, $B - I$ is diagonalizable.
An alternative approach: as the other answer notes, we can check common candidates for the eigenvectors. A matrix will have $(1,1,1)$ as an eigenvector if (and only if) all of its rows have the same sum. $B$ has an $(1,1,1)$ as an eigenvector, and the associated eigenvalue is $7$.
One way to make use of this eigenvalue/eigenvector pair is to get the characteristic polynomial of $B- 7I$. $B-7I$ is diagonalizable if and only if $B$ is diagonalizable, but because $B - 7I$ has zero as an eigenvalue, the characteristic polynomial will necessarily have a zero constant term, making it much easier to factor than the polynomial you would get through straightforward calculation. We calculate $$ \det((B - 7I) - \lambda I) = -\lambda^3 - 18 \lambda^2 - 36\lambda = -\lambda(\lambda + 6)^2, $$ which allows you to deduce that the remaining eigenvalue of $B - 7I$ is $-6$ with algebraic multiplicity $2$. Compare to the computation $$ \det(B - \lambda I) = -\lambda^3 + 9 \lambda^2 - 15\lambda + 7, $$ which we can deduce has $(\lambda - 7)$ as a factor from the fact that $7$ is an eigenvalue of $B$.
A faster (but more advanced and less generalizable) way to make use of the information that $(1,1,1)$ is an eigenvector with associated eigenvalue $7$ is to consider the eigenvalues of $B^T$. If $B$ has an eigenvalue not equal to $7$ that has a two-dimensional associated eigenspace, then it would follows that the associated eigenspace is $(1,1,1)^\perp$. We can confirm that this is indeed the case by calculating $B^Tv$ for $v = (1,-1,0),(1,0,-1)$ since these vectors form a basis of $(1,1,1)^\perp$. Indeed, $$ B^T \pmatrix{1\\-1\\0} = \pmatrix{1\\-1\\0}, \quad B^T \pmatrix{1\\0\\-1} = \pmatrix{1\\0\\-1}. $$
In this way, we have verified that there is another eigenvalue with geometric multiplicity 2 without first calculating that eigenvalue!
For the non-diagonalizable matrix $C = [T_3]_{\mathcal B}$, there's no great way to see that it won't be diagonalizable. We can speed up the process of finding the characteristic polynomial, however, by noticing that just like last time, our matrix has $(1,1,1)$ as an eigenvector, associated this time with the eigenvalue $1$. We can then calculate $\det((B - I) - \lambda I)$, which is easier to factor because of its zero constant term.
We see that $B - I$ has $3$ as an eigenvalue (corresponding to the eigenvalue $4$ of $B$) with algebraic multiplicity $2$. Notice that $B - 4I = (B - I) - 3I$ is not a rank-1 matrix, which means that the geometric multiplicity of the eigenvalue is $1$, which means that the matrix is not diagonalizable.
$T_1$ is diagonalizable with complex eigenvalues. $T_2$ is diagonalizable, $T_3$ is not.
I have some tricks for you.
if the sum of the values in each row of a matrix equal the same number then $\pmatrix {1\\1\\1}$ is an eigenvector and whatever is the sum of the rows is an eigenvalue. This will give you one eigenvalue and one eigenvector for $T_2$ and $T_3.$
The sum of the eigenvalues equals the trace of the matrix.
The product of the eigenvalues equals the determinant of the matrix.
For $T_2$ the trace is 9, the determinant is 7 and we know that 7 is an eigenvalue. For $T_3$ the trace is $6$ the determinant is $4$ and we know that $4$ is an eigenvalue.
This will quickly suggests that the eigenvalues of $T_2$ and $T_3$ are $(7,1,1)$ and $(4,1,1)$ respectively.
If we have 3 distinct eigenvalues, the matrix is diagonal, if we have a multiplicity, then it might not be.
You might also note that $T_3 - \lambda$ has row $1$ equal to row $2$ while $T_3 - 4\lambda$ has row $1$ equal to row $4$
And, $T_2 - \lambda$ has 3 identical rows.
As $T_2 - I$ gives a matrix with 3 identical rows. This indicates 2 eigenvectors associated with this eigenvalue. We have 3 eigenvectors for this matrix.
$T_3 - I$ does not suggest 2 eigenvectors for this eigenvalue and hence is not diagonalizable.
$T_1$ you might note has some resemblance to a rotation matrix, suggesting complex eigenvalues. The resemblance becomes more apparent when you calculate the determinant by an expansion of minors. It should also be obvious that $-1$ is an eigenvalue of this matrix.
